
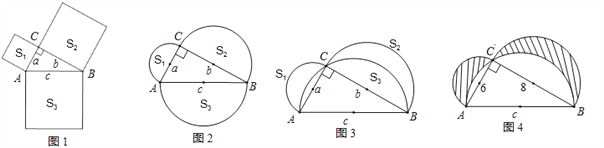
【題目】已知:在Rt△ABC中,∠C=90°∠A、∠B、∠C所對的邊分別記作a、b、c.
(1)如圖1,分別以△ABC的三條邊為邊長向外作正方形,其正方形的面積由小到大分別記作S1、S2、S3,則有____________;
(2)如圖2,分別以△ABC的三條邊為直徑向外作半圓,其半圓的面積由小到大分別記作S1、S2、S3,請問S1+S2與S3有怎樣的數量關系,并證明你的結論;
(3)分別以直角三角形的三條邊為直徑作半圓,如圖3所示,其面積由小到大分別記作S1、S2、S3,根據(2)中的探索,直接回答S1+S2與S3有怎樣的數量關系;
(4)若Rt△ABC中,AC=6,BC=8,求出圖4中陰影部分的面積.
【答案】(1)S1+S2=S3;(2)![]() ;(3)
;(3)![]() ;(4)24cm
;(4)24cm![]() .
.
【解析】試題分析:(1)根據勾股定理即可得到a,b,c滿足的關系.
(2)根據正方形的面積公式結合勾股定理就可發現大正方形的面積是兩個小正方形的面積和;
(3)分別表示出S1、S2、S3,結合勾股定理即可得出關系式.
(4)根據半圓的面積公式以及勾股定理就可發現:兩個小半圓的面積和等于大半圓的面積,從而得出陰影部分的面積=直角三角形的面積.
試題解析:(1)根據勾股定理可得S1+S2=S3.
(2)由題意得,S1=b2,S2=a2,S3=c2,∵a2+b2=c2,∴S1+S2=S3.
(3)S1=![]() ×b2,S2=
×b2,S2=![]() ×a2,S3=
×a2,S3=![]() ×c2,∵a2+b2=c2,∴S1+S2=S3.
×c2,∵a2+b2=c2,∴S1+S2=S3.
(4)因為a2+b2=c2,兩邊同乘以![]() ,即得兩小半圓的面積和等于大半圓的面積,
,即得兩小半圓的面積和等于大半圓的面積,
從而可得S陰影部分的面積=S直角三角形的面積=![]() ×8×6=24.故陰影部分的面積是24.
×8×6=24.故陰影部分的面積是24.


科目:初中數學 來源: 題型:
【題目】為選派一名學生參加全市實踐活動技能競賽,A.B兩位同學在學校實習基地現場進行加工直徑為20mm的零件的測試,他倆各加工的10個零件的相關數據依次如下圖表所示(單位:mm)
平均數 | 方差 | 完全符合要求個數 | |
A | 20 | 0.026 | 2 |
B | 20 | SB2 |
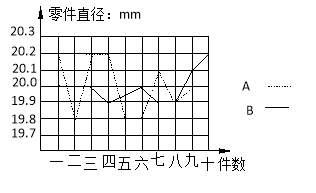
根據測試得到的有關數據,試解答下列問題:
⑴ 考慮平均數與完全符合要求的個數,你認為 的成績好些;
⑵ 計算出SB2的大小,考慮平均數與方差,說明誰的成績好些;
⑶ 考慮圖中折線走勢及競賽中加工零件個數遠遠超過10個的實際情況,你認為派誰去參賽較合適?說明你的理由。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2015年3月3日到3月15日,兩會在京矩形,霧霾防治問題受到國民的普遍關注,某報社決定以“對于霧霾,你最關注的話題是什么”為主題,通過街頭隨訪和網絡調查兩種方式進行調查,根據調查所得數據繪制了表格.
最關注的話題 | 街頭隨訪/人 | 網絡調查/人 | 合計/人 |
霧霾是什么 | 120 | 200 | |
霧霾治理 | 40%a | 60%a | a |
霧霾中自我防護策略 | 600 | ||
其他話題 | 60 |
(1)參加本次街頭隨訪和網絡調查的總人數是多少人,a的值為多少;
(2)請你將以上表格中空白處補充完整;
(3)若在接受街頭隨訪的人員中隨機抽出一人,則抽到最關注“霧霾中自我防護策略”人員的概率是 多少? ;
查看答案和解析>>
科目:初中數學 來源: 題型:
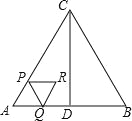
【題目】如圖,△ABC是等邊三角形,AB=4cm,CD⊥AB于點D,動點P從點A出發,沿AC以2cm/s的速度向終點C運動,當點P出發后,過點P作PQ∥BC交折線AD﹣DC于點Q,以PQ為邊作等邊三角形PQR,設四邊形APRQ與△ACD重疊部分圖形的面積為S(cm2),點P運動的時間為t(s).
(1)當點Q在線段AD上時,用含t的代數式表示QR的長;
(2)求點R運動的路程長;
(3)當點Q在線段AD上時,求S與t之間的函數關系式;
(4)直接寫出以點B、Q、R為頂點的三角形是直角三角形時t的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某超市用3 000元購進某種干果銷售,由于銷售狀況良好,超市又調撥9 000元購進該種干果,但這次的進價比第一次的進價提高了20%,購進干果數量比第一次的2倍還多300 kg.如果超市按9元/kg的價格出售,當大部分干果售出后,余下的600 kg按售價的八折售完.
(1)該種干果第一次的進價是多少?
(2)超市銷售這種干果共盈利多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
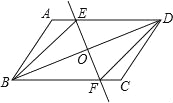
【題目】已知:如圖,在ABCD中,O為對角線BD的中點,過點O的直線EF分別交AD,BC于E,F兩點,連結BE,DF.
(1)求證:△DOE≌△BOF;
(2)當∠DOE等于多少度時,四邊形BFDE為菱形?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知AE=CF,∠AFD=∠CEB,那么添加下列一個條件后,仍無法判定△ADF≌△CBE的是( )
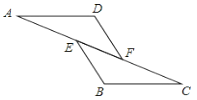
A. ∠A=∠C B. AD=CB C. BE=DF D. AD∥BC
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com