
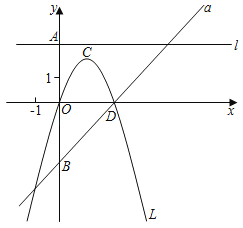
【題目】如圖,若b是正數.直線l:y=b與y軸交于點A,直線a:y=x﹣b與y軸交于點B;拋物線L:y=﹣x2+bx的頂點為C,且L與x軸右交點為D.
(1)若AB=6,求b的值,并求此時L的對稱軸與a的交點坐標;
(2)當點C在l下方時,求點C與l距離的最大值;
(3)設x0≠0,點(x0,y1),(x0,y2),(x0,y3)分別在l,a和L上,且y3是y1,y2的平均數,求點(x0,0)與點D間的距離;
(4)在L和a所圍成的封閉圖形的邊界上,把橫、縱坐標都是整數的點稱為“美點”,分別直接寫出b=2019和b=2019.5時“美點”的個數.
【答案】(1)L的對稱軸x=1.5,L的對稱軸與a的交點為(1.5,﹣1.5 );(2)1;(3)![]() ;(4)b=2019時“美點”的個數為4040個,b=2019.5時“美點”的個數為1010個.
;(4)b=2019時“美點”的個數為4040個,b=2019.5時“美點”的個數為1010個.
【解析】
(1)當x=0時,y=x﹣b=﹣b,所以B (0,﹣b),而AB=6,而A(0,b),則b﹣(﹣b)=6,b=3.所以L:y=﹣x2+3x,對稱軸x=1.5,當x=1.5吋,y=x﹣3=﹣1.5,于是得到結論.
(2)由y=﹣(x﹣![]() )2+
)2+![]() ,得到L的頂點C(
,得到L的頂點C(![]() ,
,![]() ),由于點C在l下方,于是得到結論;
),由于點C在l下方,于是得到結論;
(3)由題意得到y3=![]() ,即y1+y2=2y3,得b+x0﹣b=2(﹣x02+bx0)解得x0=0或x0=b﹣
,即y1+y2=2y3,得b+x0﹣b=2(﹣x02+bx0)解得x0=0或x0=b﹣![]() .但x0≠0,取x0=b﹣
.但x0≠0,取x0=b﹣![]() ,得到右交點D(b,0).于是得到結論;
,得到右交點D(b,0).于是得到結論;
(4)①當b=2019時,拋物線解析式L:y=﹣x2+2019x直線解析式a:y=x﹣2019,美點”總計4040個點,②當b=2019.5時,拋物線解析式L:y=﹣x2+2019.5x,直線解析式a:y=x﹣2019.5,“美點”共有1010個.
解:(1)當x=0時,y=x﹣b=﹣b,
∴B (0,﹣b),
∵AB=6,而A(0,b),
∴b﹣(﹣b)=6,
∴b=3.
∴L:y=﹣x2+3x,
∴L的對稱軸x=1.5,
當x=1.5吋,y=x﹣3=﹣1.5,
∴L的對稱軸與a的交點為(1.5,﹣1.5 );
(2)y=﹣(x﹣![]() )2+
)2+![]()
∴L的頂點C(img src="http://thumb.zyjl.cn/questionBank/Upload/2020/11/27/16/06e66ec6/SYS202011271613427160598622_DA/SYS202011271613427160598622_DA.002.png" width="16" height="41" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />,![]() ),
),
∵點C在l下方,
∴C與l的距離b﹣![]() =﹣
=﹣![]() (b﹣2)2+1≤1,
(b﹣2)2+1≤1,
∴點C與1距離的最大值為1;
(3)由題意得y3=![]() ,即y1+y2=2y3,
,即y1+y2=2y3,
得b+x0﹣b=2(﹣x02+bx0)
解得x0=0或x0=b﹣![]() .但x0≠0,取x0=b﹣
.但x0≠0,取x0=b﹣![]() ,
,
對于L,當y=0吋,0=﹣x2+bx,即0=﹣x(x﹣b),
解得x1=0,x2=b,
∵b>0,
∴右交點D(b,0).
∴點(x0,0)與點D間的距離b﹣(b﹣![]() )=
)=![]() ;
;
(4)①當b=2019時,拋物線解析式L:y=﹣x2+2019x,
直線解析式a:y=x﹣2019
聯立上述兩個解析式可得:x1=﹣1,x2=2019,
∴可知每一個整數x的值都對應的一個整數y值,且﹣1和2019之間(包括﹣1和﹣2019)共有2021個整數;
∵另外要知道所圍成的封閉圖形邊界分兩部分:線段和拋物線,
∴線段和拋物線上各有2021個整數點,
∴總計4042個點,
∵這兩段圖象交點有2個點重復,
∴美點”的個數:4042﹣2=4040(個);
②當b=2019.5時,
拋物線解析式L:y=﹣x2+2019.5x,
直線解析式a:y=x﹣2019.5,
聯立上述兩個解析式可得:x1=﹣1,x2=2019.5,
∴當x取整數時,在一次函數y=x﹣2019.5上,y取不到整數值,因此在該圖象上“美點”為0,
在二次函數y=x2+2019.5x圖象上,當x為偶數時,函數值y可取整數,
可知﹣1到2019.5之 間有1010個偶數,因此“美點”共有1010個.
故b=2019時“美點”的個數為4040個,b=2019.5時“美點”的個數為1010個.


科目:初中數學 來源: 題型:
【題目】已知二次函數y=ax2+bx﹣3a經過點A(﹣1,0)、C(0,3),與x軸交于另一點B,拋物線的頂點為D.

(1)求此二次函數解析式;
(2)連接DC、BC、DB,求證:△BCD是直角三角形;
(3)在對稱軸右側的拋物線上是否存在點P,使得△PDC為等腰三角形?若存在,求出符合條件的點P的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,學校環保社成員想測量斜坡CD旁一棵樹AB的高度,他們先在點C處測得樹頂B的仰角為 60°,然后在坡頂D測得樹頂B的仰角為300,已知斜坡CD的長度為20m,DE的長為10m,則樹AB的高度是( ) m

A. ![]() B. 30 C.
B. 30 C. ![]() D. 40
D. 40
查看答案和解析>>
科目:初中數學 來源: 題型:
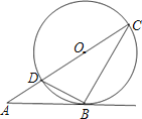
【題目】如圖,DC是⊙O的直徑,點B在圓上,直線AB交CD延長線于點A,且∠ABD=∠C.
(1)求證:AB是⊙O的切線;
(2)若AB=4cm,AD=2cm,求tanA的值和DB的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,已知△ABC的三個頂點的坐標分別是A(﹣4,1),B(﹣1,2),C(﹣2,4).
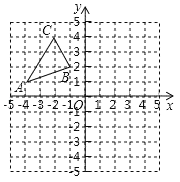
(1)將△ABC向右平移4個單位后得到△A1B1C1,請畫出△A1B1C1,并寫出點B1的坐標;
(2)△A2B2C2和△A1B1C1關于原點O中心對稱,請畫出△A2B2C2,并寫出點C2的坐標;
(3)連接點A和點B2,點B和點A2,得到四邊形AB2A2B,試判斷四邊形AB2A2B的形狀(無須說明理由).
查看答案和解析>>
科目:初中數學 來源: 題型:
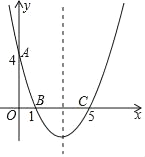
【題目】如圖,在直角坐標系中,拋物線經過點A(0,4),B(1,0),C(5,0)
(1)求拋物線的解析式和對稱軸;
(2)在拋物線的對稱軸上是否存在一點P,使△PAB的周長最小?若存在,請求出點P的坐標;若不存在,請說明理由;
(3)該拋物線有一點D(x,y),使得S△ABC=S△DBC,求點D的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC 中,AB=AC, ∠BAC <60°,將線段 AB 繞點 A逆時針旋轉 60°得到點 D, 點 E 與點 D 關于直線 BC 對稱,連接 CD,CE,DE.
(1)依題意補全圖形;
(2)判斷△CDE 的形狀,并證明;
(3)請問在直線CE上是否存在點 P,使得 PA - PB =CD 成立?若存在,請用文字描述出點 P 的準確位置,并畫圖證明;若不存在,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線![]() 與
與![]() 軸交于
軸交于![]() 兩點(點
兩點(點![]() 在 點
在 點![]() 左側),對稱軸為直線
左側),對稱軸為直線![]() .
.
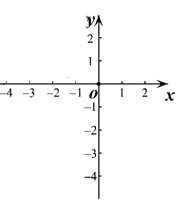
(1)![]() 的值為 ,在坐標系中利用描點法畫出此拋物線;
的值為 ,在坐標系中利用描點法畫出此拋物線;
| ··· | ··· | |||||
| ··· | ··· |
(2)若直線![]() 過點
過點![]() 且與拋物線交于點
且與拋物線交于點![]() ,請根據圖象寫出:當
,請根據圖象寫出:當![]() 時,
時,![]() 的取值范圍是 .
的取值范圍是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知![]() 中,
中,![]() ,D是線段AC上一點(不與A,C重合),連接BD,將
,D是線段AC上一點(不與A,C重合),連接BD,將![]() 沿AB翻折,使點D落在點E處,延長BD與EA的延長線交于點F,若
沿AB翻折,使點D落在點E處,延長BD與EA的延長線交于點F,若![]() 是直角三角形,則AF的長為_________.
是直角三角形,則AF的長為_________.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com