
【題目】如圖所示,在△ABC中,AB=AC,BD⊥AC于D,CE⊥AB于E,BD,CE相交于F.
求證:AF平分∠BAC.

【答案】證明見解析
【解析】試題分析:先根據AB=AC,可得∠ABC=∠ACB,再由垂直,可得90°的角,在△BCE和△BCD中,利用內角和為180°,可分別求∠BCE和∠DBC,利用等量減等量差相等,可得FB=FC,再易證△ABF≌△ACF,從而證出AF平分∠BAC.
試題解析:證明:∵AB=AC(已知),
∴∠ABC=∠ACB(等邊對等角).
∵BD、CE分別是高,
∴BD⊥AC,CE⊥AB(高的定義).
∴∠CEB=∠BDC=90°.
∴∠ECB=90°∠ABC,∠DBC=90°∠ACB.
∴∠ECB=∠DBC(等量代換).
∴FB=FC(等角對等邊),
在△ABF和△ACF中,
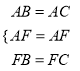 ,
,
∴△ABF≌△ACF(SSS),
∴∠BAF=∠CAF(全等三角形對應角相等),
∴AF平分∠BAC.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖,在數軸上有A、B、C、D四個整數點(即各點均表示整數),且2AB=BC=3CD,若A、D兩點表示的數分別為﹣5和6,且AC的中點為E,BD的中點為M,BC之間距點B的距離為![]() BC的點N,則該數軸的原點為( )
BC的點N,則該數軸的原點為( )
![]()
A. 點E B. 點F C. 點M D. 點N
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了鼓勵送彩電下鄉,國家決定對購買彩電的農戶實行政府補貼.規定每購買一臺彩電,政府補貼若干元,經調查某商場銷售彩電臺數y(臺)與補貼款額x(元)之間大致滿足如圖①所示的一次函數關系.隨著補貼款額x的不斷增大,銷售量也不斷增加,但每臺彩電的收益Z(元)會相應降低且Z與x之間也大致滿足如圖②所示的一次函數關系。
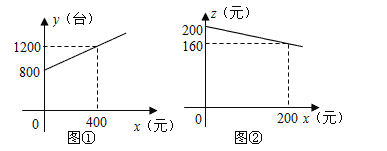
(1)在政府未出臺補貼措施前,該商場銷售彩電的總收益額為多少元?
(2)在政府補貼政策實施后,分別求出該商場銷售彩電臺數y和每臺家電的收益z與政府補貼款額x之間的函數關系式;
(3)要使該商場銷售彩電的總收益w(元)最大,政府應將每臺補貼款額x定為多少并求出總收益w的最大值。
查看答案和解析>>
科目:初中數學 來源: 題型:
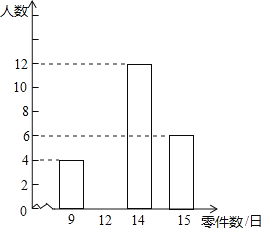
【題目】某車間有120名工人,為了了解這些工人日加工零件數的情況,隨機抽出其中的30名工人進行調查.整理調查結果,繪制出不完整的條形統計圖(如圖).根據圖中的信息,解答下列問題:
(1)在被調查的工人中,日加工9個零件的人數為 名;
(2)在被調查的工人中,日加工12個零件的人數為 名,日加工 個零件的人數最多,日加工15個零件的人數占被調查人數的 %;
(3)依據本次調查結果,估計該車間日人均加工零件數和日加工零件的總數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知點P為∠AOB的角平分線上的一點,點D在邊OA上.愛動腦筋的小剛經過仔細觀察后,進行如下操作:在邊OB上取一點E,使得PE=PD,這時他發現∠OEP與∠ODP之間有一定的數量關系,請你寫出∠OEP與∠ODP所有可能的數量關系是 .

查看答案和解析>>
科目:初中數學 來源: 題型:
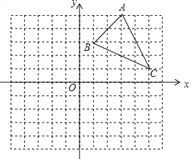
【題目】如圖,方格紙中的每個小方格都是邊長為1個單位的正方形,在建立平面直角坐標系后,△ABC的頂點均在格點上,點C的坐標為(5,1).
①畫出△ABC關于y軸對稱的△A1B1C1,并寫出點C1的坐標;
②連結BC1,在坐標平面的格點上確定一個點P,使△B C1P是以B C1為底的等腰直角三角形,畫出△B C1P,并寫出所有P點的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com