
【題目】堅持節約資源和保護環境是我國的基本國策,國家要求加強生活垃圾分類回收與再生資源回收有效銜接,提高全社會資源產出率,構建全社會的資源循環利用體系.
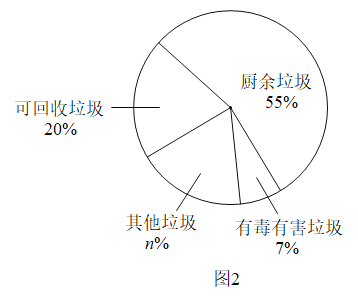
圖1反映了2014—2019年我國生活垃圾清運量的情況.

圖2反映了2019年我國G市生活垃圾分類的情況.
根據以上材料回答下列問題:
(1)圖2中,n的值為___________;
(2)2014—2019年,我國生活垃圾清運量的中位數是_________;
(3)據統計,2019年G市清運的生活垃圾中可回收垃圾約為0.02億噸,所創造的經濟總價值約為40億元.若2019年我國生活垃圾清運量中,可回收垃圾的占比與G市的占比相同,根據G市的數據估計2019年我國可回收垃圾所創造的經濟總價值是多少.
【答案】(1)18;(2)2.1;(3)1000億元.
【解析】
(1)直接利用![]() 減去廚余垃圾、可回收垃圾、有毒有害垃圾的占比即可得;
減去廚余垃圾、可回收垃圾、有毒有害垃圾的占比即可得;
(2)根據中位數的定義即可得;
(3)先根據可回收垃圾的占比求出2019年我國生活垃圾清運量中可回收垃圾的量,再求出每1億噸可回收垃圾所創造的經濟總價值,然后乘以可回收垃圾的量即可得.
(1)![]()
解得![]()
故答案為:18;
(2)由圖1可知,2014—2019年,我國生活垃圾清運量依次為![]()
則中位數為![]()
故答案為:![]() ;
;
(3)由題意:2019年我國生活垃圾清運量中可回收垃圾量為![]() (億噸)
(億噸)
每1億噸可回收垃圾所創造的經濟總價值為![]() (億元/億噸)
(億元/億噸)
則![]() (億元)
(億元)
答:根據G市的數據估計2019年我國可回收垃圾所創造的經濟總價值是1000億元.


 53隨堂測系列答案
53隨堂測系列答案科目:初中數學 來源: 題型:
【題目】已知關于x的二次函數y=ax2﹣4ax+a+1(a>0)
(1)若二次函數的圖象與x軸有交點,求a的取值范圍;
(2)若P(m,n)和Q(5,b)是拋物線上兩點,且n>b,求實數m的取值范圍;
(3)當m≤x≤m+2時,求y的最小值(用含a、m的代數式表示).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某市教育行政部門為了解初中學生參加綜合實踐活動的情況,隨機抽取了本市初一、初二、初三年級各![]() 名學生進行了調查,調查結果如圖所示,請你根據圖中的信息回答問題.
名學生進行了調查,調查結果如圖所示,請你根據圖中的信息回答問題.

(1)在被調查的學生中,參加綜合實踐活動的有多少人,參加科技活動的有多少人;
(2)如果本市有![]() 萬名初中學生,請你估計參加科技活動的學生約有多少名.
萬名初中學生,請你估計參加科技活動的學生約有多少名.
查看答案和解析>>
科目:初中數學 來源: 題型:
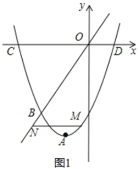
【題目】已知拋物線的頂點![]() ,經過點
,經過點![]() ,與
,與![]() 軸分別交于
軸分別交于![]() ,
,![]() 兩點.
兩點.
(1)求該拋物線的解析式;
(2)如圖1,點![]() 是拋物線上的一個動點,且在直線
是拋物線上的一個動點,且在直線![]() 的下方,過點
的下方,過點![]() 作
作![]() 軸的平行線與直線
軸的平行線與直線![]() 交于點
交于點![]() ,當
,當![]() 取最大值時,求點
取最大值時,求點![]() 的坐標;
的坐標;
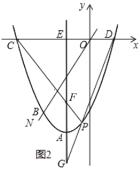
(3)如圖2,![]() 軸交
軸交![]() 軸于點
軸于點![]() ,點
,點![]() 是拋物線上
是拋物線上![]() ,
,![]() 之間的一個動點,直線
之間的一個動點,直線![]() ,
,![]() 與
與![]() 分別交于
分別交于![]() ,
,![]() ,當點
,當點![]() 運動時.
運動時.
①直接寫出![]() 的值;
的值;
②直接寫出![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,拋物線
中,拋物線![]() 與x軸的交點為A,B,與y軸交于C.
與x軸的交點為A,B,與y軸交于C.
(1)求拋物線的對稱軸和點C坐標;
(2)橫、縱坐標都是整數的點叫做整點.拋物線在點A,B之間的部分與線段![]() 所圍成的區域為圖形W(不含邊界).
所圍成的區域為圖形W(不含邊界).
①當![]() 時,求圖形W內的整點個數;
時,求圖形W內的整點個數;
②若圖形W內有2個整數點,求m的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面內,對于給定的![]() ,如果存在一個半圓或優弧與
,如果存在一個半圓或優弧與![]() 的兩邊相切,且該弧上的所有點都在
的兩邊相切,且該弧上的所有點都在![]() 的內部或邊上,則稱這樣的弧為
的內部或邊上,則稱這樣的弧為![]() 的內切弧.當內切弧的半徑最大時,稱該內切弧為
的內切弧.當內切弧的半徑最大時,稱該內切弧為![]() 的完美內切弧.(注:弧的半徑指該弧所在圓的半徑)
的完美內切弧.(注:弧的半徑指該弧所在圓的半徑)
在平面直角坐標系![]() 中,
中,![]() .
.
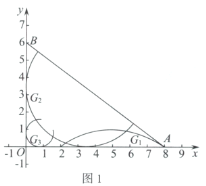
(1)如圖1,在弧![]() ,弧
,弧![]() ,弧
,弧![]() 中,是
中,是![]() 的內切弧的是____________;
的內切弧的是____________;
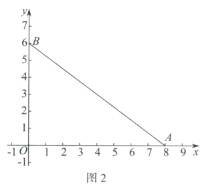
(2)如圖2,若弧G為![]() 的內切弧,且弧G與邊
的內切弧,且弧G與邊![]() 相切,求弧G的半徑的最大值;
相切,求弧G的半徑的最大值;
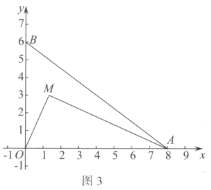
(3)如圖3,動點![]() ,連接
,連接![]() .
.
①直接寫出![]() 的完美內切弧的半徑的最大值;
的完美內切弧的半徑的最大值;
②記①中得到的半徑最大時的完美內切弧為弧T.點P為弧T上的一個動點,過點P作x軸的垂線,分別交x軸和直線![]() 于點D,E,點F為線段
于點D,E,點F為線段![]() 的中點,直接寫出線段
的中點,直接寫出線段![]() 長度的取值范圍.
長度的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某市水果批發欲將A市的一批水果運往本市銷售,有火車和汽車兩種運輸方式,運輸過程中的損耗均為200元/時,其它主要參考數據如下:
運輸工具 | 途中平均速度(千米/時) | 運費(元/千米) | 裝卸費用(元) |
火車 | 100 | 15 | 2000 |
汽車 | 80 | 20 | 900 |
(1) 如果汽車的總支出費用比火車費用多1100元,你知道本市與A市之間的路程是多少千米嗎?請你列方程解答.(總支出包含損耗、運費和裝卸費用)
(2) 如果A市與B市之間的距離為S千米,你若是A市水果批發部門的經理,要想將這種水果運往B市銷售,試分析以上兩種運輸工具中選擇哪種運輸方式比較合算呢?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在矩形![]() 中,
中,![]() ,點
,點![]() 是線段
是線段![]() 上的一個動點,以點
上的一個動點,以點![]() 為圓心,
為圓心,![]() 為半徑作
為半徑作![]() ,連接
,連接![]() .
.
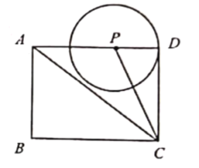
(1)當![]() 經過
經過![]() 的中點時,
的中點時,![]() 的長為_ ;
的長為_ ;
(2)當![]() 平分
平分![]() 時,判斷
時,判斷![]() 與
與![]() 的位置關系.說明理由,并求出
的位置關系.說明理由,并求出![]() 的長;
的長;
(3)如圖2,當![]() 與
與![]() 交于
交于![]() 兩點,且
兩點,且![]() 時,求點
時,求點![]() 到
到![]() 的距離.
的距離.
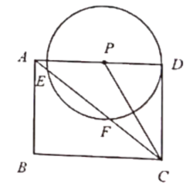
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某企業設計了一款工藝品,每件的成本是50元,為了合理定價,投放市場進行試銷.據市場調查,銷售單價是100元時,每天的銷售量是50件,而銷售單價每降低1元,每天就可多售出5件,但要求銷售單價不得低于成本.
![]() 求出每天的銷售利潤
求出每天的銷售利潤![]() 元
元![]() 與銷售單價
與銷售單價![]() 元
元![]() 之間的函數關系式;
之間的函數關系式;
![]() 求出銷售單價為多少元時,每天的銷售利潤最大?最大利潤是多少?
求出銷售單價為多少元時,每天的銷售利潤最大?最大利潤是多少?
![]() 如果該企業要使每天的銷售利潤不低于4000元,且每天的總成本不超過7000元,那么銷售單價應控制在什么范圍內?
如果該企業要使每天的銷售利潤不低于4000元,且每天的總成本不超過7000元,那么銷售單價應控制在什么范圍內?![]() 每天的總成本
每天的總成本![]() 每件的成本
每件的成本![]() 每天的銷售量
每天的銷售量![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com