
【題目】已知矩形![]() 中,
中,![]() ,
,![]() ,點
,點![]() 是邊
是邊![]() 上一點,
上一點,![]() ,連接
,連接![]() .
.
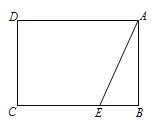
(1)沿![]() 翻折
翻折![]() 使點
使點![]() 落在點
落在點![]() 處,
處,
①連接![]() ,若
,若![]() ,求
,求![]() 的值;
的值;
②連接![]() ,若
,若![]() ,求
,求![]() 的取值范圍.
的取值范圍.
(2)![]() 繞點
繞點![]() 順時針旋轉得
順時針旋轉得![]() ,點
,點![]() 落在邊
落在邊![]() 上時旋轉停止. 若點
上時旋轉停止. 若點![]() 落在矩形對角線
落在矩形對角線![]() 上,且點
上,且點![]() 到
到![]() 的距離小于
的距離小于![]() 時,求
時,求![]() 的取值范圍.
的取值范圍.
【答案】(1)①2;②![]() ;(2)
;(2)![]() .
.
【解析】
(1)①由CF∥AE可得內錯角和同位角相等,由翻折有對應角相等,等量代換后出現等腰三角形,即可求出m值;②過點F作GH⊥AD于點G,交BC于點H,根據相似三角形的對應邊成比例求翻折后AG和FG的長度,再根據勾股定理列出DF2與m的二次函數關系根據拋物線的性質求出自變量m的范圍;
(2)過點B1作MN⊥AD于點M,交BC于點N,由△AMB1∽△CBA得出對應邊成比例列出比例式,用含m的式子表示B1M,根據題意求出m的范圍,再根據當E1落在AD上時,此時m最大,根據△AB1E1∽△ABE求出m的最大值,從而確定m的取值范圍.
解:(1)①如圖,
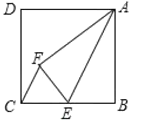
∵CF∥AE,
∴∠FCE=∠AEB, ∠CFE=∠AEF,
∵△ABE翻折得到△AFE,
∴EF=EB=1,∠AEF=∠AEB,
∴∠ECF=∠EFC,
∴CE=EF=1,
∴m=BC=BE+CE=2.
②如圖,過點F作GH⊥AD于點G,交BC于點H,
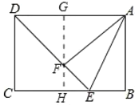
∴∠AGH=∠GHB=∠B=90°,
∴四邊形AGHB是矩形,
∴AG=BH,GH=AB=2,
由折疊可知,∠B=∠AFE=90°,BE=FE=1,AF=AB=2,
∵∠GAF+∠AFG=90°, ∠AFG+∠EFH=90°,
∴∠GAF=∠EFH,
∴△AGF∽△HFE,
∴![]() ,
,
設AG=a,GF=b,則有,
![]() ,
,
解得:a=![]() ,b=
,b=![]() ,
,
∵AD=BC=m,
∴DG=![]() =
=![]() ,
,
∴DF2=DG2+FG2=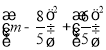 =
= 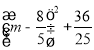 ,
,
∴DF2與m成二次函數關系,且拋物線開口向上,當m=![]() 時,DF2有最小值為
時,DF2有最小值為![]() ,
,
∵![]() ,
,
∴![]() ,
,
當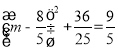 時,
時,
解得m1=1,m2=![]() ,
,
∴由二次函數圖象的性質可得,![]() .
.
(2)如圖,過點B1作MN⊥AD于點M,交BC于點N,
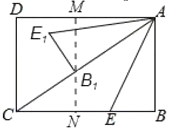
∴∠AMB1=∠B=90°,
∵AD∥BC,
∴∠MAB1=∠ACB,
∴△AMB1∽△CBA,
∴![]() ,
,
由翻折可知AB1=AB=2,
∴![]() ,
,
∴B1M=![]() ,
,
∵點B1到![]() 的距離小于
的距離小于![]() ,
,
∴![]() <
<![]() ,解得m>
,解得m>![]() .
.
如圖,當點E1落在邊AD上時,且點B1在AC上時,m最大,
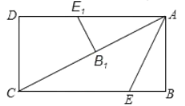
∵∠AB1E1=∠ABC, ∠E1AB=∠ACB,
∴△AB1E1∽△ABE,
∴![]() ,即
,即![]() ,
,
∴m=4,
∴m的取值范圍是![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,已知C(3,4),以點C為圓心的圓與y軸相切.點A、B在x軸上,且OA=OB.點P為⊙C上的動點,∠APB=90°,則AB長度的最大值為 _____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知正方形![]() ,點
,點![]() 是其內部一點.
是其內部一點.

(1)如圖1,點![]() 在邊
在邊![]() 的垂直平分線
的垂直平分線![]() 上,將
上,將![]() 繞點
繞點![]() 逆時針旋轉,得到
逆時針旋轉,得到![]() ,當點
,當點![]() 落在
落在![]() 上時,恰好點
上時,恰好點![]() 落在直線
落在直線![]() 上,求
上,求![]() 的度數;
的度數;
(2)如圖2,點![]() 在對角線
在對角線![]() 上,連接
上,連接![]() ,若將線段
,若將線段![]() 繞點
繞點![]() 逆時針旋轉
逆時針旋轉![]() 后得到線段
后得到線段![]() ,試問點
,試問點![]() 是否在直線
是否在直線![]() 上,請給出結論,并說明理由;
上,請給出結論,并說明理由;
(3)如圖3,若![]() ,設
,設![]() ,
,![]() ,
,![]() ,請寫出
,請寫出![]() 、
、![]() 、
、![]() 這三條線段長之間滿足的數量關系是____________.
這三條線段長之間滿足的數量關系是____________.
查看答案和解析>>
科目:初中數學 來源: 題型:
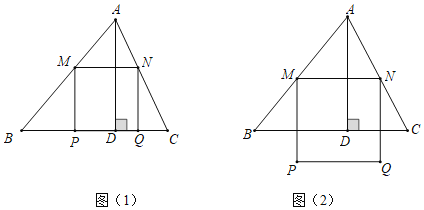
【題目】如圖在銳角△ABC中,BC=6,高AD=4,兩動點M、N分別在AB、AC上滑動(不包含端點),且MN∥BC,以MN為邊長向下作正方形MPQN,設MN=x,正方形MPQN與△ABC公共部分的面積為y.
(1)如圖(1),當正方形MPQN的邊P恰好落在BC邊上時,求x的值;
(2)如圖(2),當PQ落△ABC外部時,求出y與x的函數關系式(寫出x的取值范圍)并求出x為何值時y最大,最大是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知直線y=kx(k≠0)經過點(12,﹣5),將直線向上平移m(m>0)個單位,若平移后得到的直線與半徑為6的⊙O相交(點O為坐標原點),則m的取值范圍為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某景區經營一種新上市的紀念品,進價為20元/件.試營銷階段發現:當銷售單價是25元時,每天的銷售量為250件;銷售單價每上漲1元,每天的銷售量就減少10件.設這種紀念品的銷售單價為x(元).
(1)求每天所得的銷售利潤y(元)與銷售單價x(元)之間的函數關系式;
(2)求銷售單價為多少元時,該紀念品每天的銷售利潤最大;
(3)若要求每天銷售量不少于10件,且每件文具的利潤至少為25元,則該紀念品的最大利潤是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,二次函數![]() 的圖象記為
的圖象記為![]() ,它與x軸交于點O,
,它與x軸交于點O,![]() ;將
;將![]() 繞點
繞點![]() 旋轉
旋轉![]() 得
得![]() ,交x軸于點
,交x軸于點![]() ;將
;將![]() 繞點
繞點![]() 旋轉
旋轉![]() 得
得![]() ,交x軸于點
,交x軸于點![]() ;……如此進行下去,得到一條“波浪線”.若
;……如此進行下去,得到一條“波浪線”.若![]() 在這條“波浪線”上,則
在這條“波浪線”上,則![]() ________.
________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對于一個關于x的代數式A,若存在一個系數為正數關于x的單項式F,使![]() 的結果是所有系數均為整數的整式,則稱單項式F為代數式A的“整系單項式”.例如:
的結果是所有系數均為整數的整式,則稱單項式F為代數式A的“整系單項式”.例如:
當A=![]() ,F=2x3時,由于
,F=2x3時,由于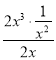 =1,故2x3是
=1,故2x3是![]() 的整系單項式;
的整系單項式;
當A=![]() ,F=6x5時,由于
,F=6x5時,由于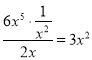 ,故6x5是
,故6x5是![]() 的整系單項式;
的整系單項式;
當A=3-![]() ,F=
,F=![]() 時,由于
時,由于 =2x-1,故
=2x-1,故![]() 是3-
是3-![]() 的整系單項式;
的整系單項式;
當A=3-![]() ,F=8x4時,由于
,F=8x4時,由于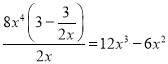 ,故8x4是3-
,故8x4是3-![]() 的整系單項式;
的整系單項式;
顯然,當代數式A存在整系單項式F時,F有無數個,現把次數最低,系數最小的整系單項式F記為F(A).例如:![]() ,
,![]()
閱讀以上材料并解決下列問題:
(1)判斷:當A=![]() 時,F=2x3______A的整系單項式(填“是”或“不是”)
時,F=2x3______A的整系單項式(填“是”或“不是”)
(2)解方程: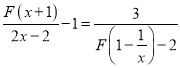
(3)已知a、b、c是△ABC的邊長,其中a、b滿足(a-5)2+![]() =0,且關于x的方程|
=0,且關于x的方程|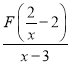 |=c有且只有3個不相等的實數根,求△ABC的周長.
|=c有且只有3個不相等的實數根,求△ABC的周長.
查看答案和解析>>
科目:初中數學 來源: 題型:
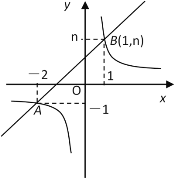
【題目】如圖,一次函數![]() 的圖象與反比例函數
的圖象與反比例函數![]() 的圖象交于A(-2,-1)、B(1,n)兩點。
的圖象交于A(-2,-1)、B(1,n)兩點。
(1)利用圖中條件求反比例函數和一次函數的解析式;
(2)根據圖象寫出使一次函數的值大于反比例函數的值的![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com