
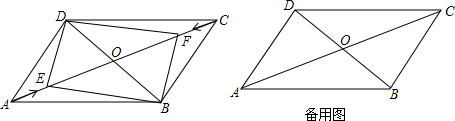
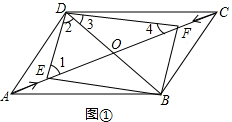
 解:(1)由題意得:AE=CF=tcm.
解:(1)由題意得:AE=CF=tcm.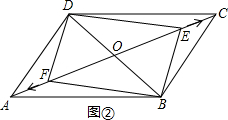
 BD=5cm.
BD=5cm. (AC-EF)=
(AC-EF)= (14-10)=2cm或AE=CF=14-2=12cm
(14-10)=2cm或AE=CF=14-2=12cm BD=5cm.然后由平行四邊形DEBF的對角線的性質來求AE=CF的值.
BD=5cm.然后由平行四邊形DEBF的對角線的性質來求AE=CF的值.

 全能測控期末小狀元系列答案
全能測控期末小狀元系列答案科目:初中數學 來源: 題型:
 如圖,在?ABCD中,對角線AC、BD相交于點O,AB=
如圖,在?ABCD中,對角線AC、BD相交于點O,AB=| 29 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com