如圖，在平面直角坐標系xOy中，矩形ABCD的邊AD=6，A（1，0）， B（9，0），直線y=kx+b經過B、D兩點．
（1）求直線y=kx+b的表達式；
（2）將直線y=kx+b平移，當它與矩形沒有公共點時，直接寫出b的取值范圍．
科目：初中數學 來源： 題型：解答題
在一條筆直的公路旁依次有A、B、C三個村莊，甲、乙兩人同時分別從A、B兩村出發，甲騎摩托車，乙騎電動車沿公路勻速駛向C村，最終到達C村．設甲、乙兩人到C村的距離y1，y2（km）與行駛時間x（h）之間的函數關系如圖所示，請回答下列問題：
（1）A、C兩村間的距離為 km，a= ；
（2）求出圖中點P的坐標，并解釋該點坐標所表示的實際意義；
（3）乙在行駛過程中，何時距甲10km？
查看答案和解析>>
科目：初中數學 來源： 題型：解答題
已知A、B兩地相距300千米，甲、乙兩車同時從A地出發，以各自的速度勻速往返兩地，甲車先到達B地，停留1小時后按原路返回．設兩車行駛的時間為x小時，離開A地的距離是y千米，如圖是y與x的函數圖象．
(1)計算甲車的速度為 千米／時，乙車的速度為 千米／時；
(2)幾小時后兩車相遇；
(3)在從開始出發到兩車相遇的過程中，設兩車之間的距離為S千米，乙車行駛的時間為t小時，求S與t之間的函數關系式．
查看答案和解析>>
科目：初中數學 來源： 題型：解答題
設
，
是任意兩個不等實數，我們規定：滿足不等式≤
≤
的實數的所有取值的全體叫做閉區間，表示為
. 對于一個函數，如果它的自變量與函數值
滿足：當m≤≤n時，有m≤≤n，我們就稱此函數是閉區間
上的“閉函數”.
（1）反比例函數
是閉區間
上的“閉函數”嗎？請判斷并說明理由；
（2）若一次函數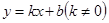
是閉區間上的“閉函數”，求此函數的表達式；
（3）若二次函數
是閉區間上的“閉函數”，直接寫出實數， 的值.
查看答案和解析>>
科目：初中數學 來源： 題型：解答題
在學習三角形中線的知識時，小明了解到：三角形的任意一條中線所在的直線可以把該三角形分為面積相等的兩部分。進而，小明繼續研究，過四邊形的某一頂點的直線能否將該四邊形平分為面積相等的兩部分？他畫出了如下示意圖（如圖1），得到了符合要求的直線AF.
小明的作圖步驟如下：
第一步：連結AC；
第二步：過點B作BE//AC交DC的延長線于點E；
第三步：取ED中點F，作直線AF；
則直線AF即為所求.
請參考小明思考問題的方法，解決問題：
如圖2，五邊形ABOCD，各頂點坐標為：A(3,4)，B(0,2)，O(0,0)，C(4,0)，D(4,2).請你構造一條經過頂點A的直線，將五邊形ABOCD分為面積相等的兩部分，并求出該直線的解析式.
查看答案和解析>>
科目：初中數學 來源： 題型：解答題
如圖，一次函數y＝kx＋3的圖象分別交x軸、y軸于點C、點D，與反比例函數
的圖象在第四象限相交于點P，并且PA⊥x軸于點A，PB⊥y軸于點B，已知B（0，－6）且S△DBP＝27.
（1）求上述一次函數與反比例函數的表達式；
（2）設點Q是一次函數y＝kx＋3圖象上的一點，且滿足△DOQ的面積是△COD面積的2倍，直接寫出點Q的坐標.
（3）若反比例函數
的圖象與△ABP總有公共點，直接寫出n的取值范圍.
查看答案和解析>>
科目：初中數學 來源： 題型：解答題
已知一次函數
的圖象經過點（
，
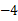），且與正比例函數
的圖象相交于點（4，
），
求：（1）的值；
（2）
、
的值；
（3）求出這兩個函數的圖象與
軸相交得到的三角形的面積．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
；（2）
或
.
，當它左移超過點A或右移超過點C時，它與矩形沒有公共點 .因此，只要將A， C兩點坐標分別代入
的值即可求得b的取值范圍
，解得 
.
經過點(1，－1)，求關于x的不等式2x－b≥0的解集.