
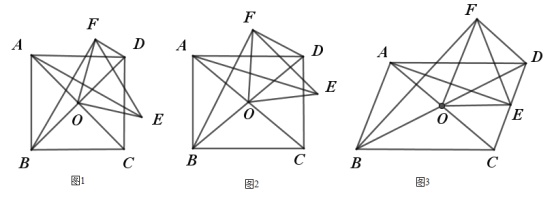
【題目】如圖1,正方形ABCD的對角線AC,BD交于點O,將△COD繞點O逆時針旋轉得到△EOF(旋轉角為銳角),連AE,BF,DF,則AE=BF.
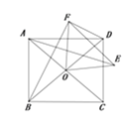
(1)如圖2,若(1)中的正方形為矩形,其他條件不變.
①探究AE與BF的數量關系,并證明你的結論;
②若BD=7,AE=![]() ,求DF的長;
,求DF的長;
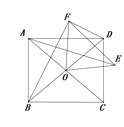
(2)如圖3,若(1)中的正方形為平行四邊形,其他條件不變,且BD=10,AC=6,AE=5,請直接寫出DF的長.
【答案】(1)①AE=BF;證明見解析;②DF=![]() ;(2)DF=
;(2)DF=![]() .
.
【解析】
(1)①利用矩形的性質,旋轉的性質得到∠BOF=∠AOE,證明△BOF≌△AOE可得結論,
②利用矩形性質與旋轉性質證明△BFD為直角三角形,從而可得答案,
(2)利用平行四邊形的性質與旋轉的性質,證明△AOE∽△BOF,求解BF,再證明△BDF是直角三角形,從而可得答案.
(1)①AE=BF,理由如下:
證明:∵ABCD為矩形,
∴AC=BD,OA=OB=OC=OD,
∵△COD繞點O旋轉得△EOF,
∴OC=OE,OD=OF,∠COE=∠DOF
∵∠BOD=∠AOC=180°
∴∠BOD-∠DOF=∠AOC-∠COE
即∠BOF=∠AOE
∴△BOF≌△AOE(SAS),
∴BF=AE
②∵OB=OD=OF,
∴∠BFD=90°
∴△BFD為直角三角形,
∴![]() ,
,
∵BF=AE
∴![]()
∵BD=7,AE=![]()
∴DF=![]()
(2))∵四邊形ABCD是平行四邊形,
∴OC=OA=![]() AC=3,OB=OD=
AC=3,OB=OD=![]() BD=5,
BD=5,
∵將△COD繞點O按逆時針方向旋轉得到△FOE,
∴OC=OE,OD=OF,∠EOC=∠FOD
∴OA=OE,OB=OF,∠EOA=∠FOB
∴ ![]() ,且∠EOA=∠FOB
,且∠EOA=∠FOB
∴△AOE∽△BOF,
∴ ![]()
![]()
![]()
∵OB=OF=OD
∴△BDF是直角三角形,
∴![]()
![]()


科目:初中數學 來源: 題型:
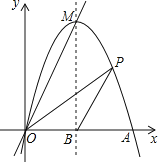
【題目】如圖,拋物線![]() 交
交![]() 軸正半軸于點
軸正半軸于點![]() ,直線
,直線![]() 經過拋物線的頂點
經過拋物線的頂點![]() .已知該拋物線的對稱軸為直線
.已知該拋物線的對稱軸為直線![]() ,交
,交![]() 軸于點
軸于點![]() .
.
(1)求![]() 的值.
的值.
(2)![]() 是第一象限內拋物線上的一點,且在對稱軸的右側,連接
是第一象限內拋物線上的一點,且在對稱軸的右側,連接![]() .設點
.設點![]() 的橫坐標為
的橫坐標為![]() ;
;
①![]() 的面積為
的面積為![]() ,用含
,用含![]() 的式子表示
的式子表示![]() ;
;
②記![]() .求
.求![]() 關于
關于![]() 的函數表達式及
的函數表達式及![]() 的范圍.
的范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
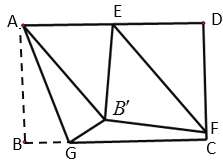
【題目】如圖,在矩形![]() 中,
中,![]() ,
,![]() ,點
,點![]() 是
是![]() 的中點,點
的中點,點![]() 是線段
是線段![]() 的一個動點,點
的一個動點,點![]() 是線段
是線段![]() 上的點,
上的點,![]() ,連接
,連接![]() 將
將![]() 沿
沿![]() 翻折,點
翻折,點![]() 的對應點為點
的對應點為點![]() ,連接
,連接![]() ,
,![]() ,若
,若![]() 為直角三角形,則
為直角三角形,則![]() 為________.
為________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校為了解九年級學生新冠疫情防控期間每天居家體育活動的時間(單位:![]() ),在網上隨機調查了該校九年級部分學生.根據調查結果,繪制出如下的統計圖1和圖2.請根據相關信息,解答下列問題:
),在網上隨機調查了該校九年級部分學生.根據調查結果,繪制出如下的統計圖1和圖2.請根據相關信息,解答下列問題:
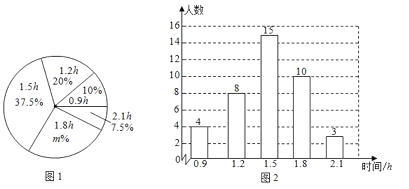
(1)本次接受調查的初中學生人數為________,圖①中![]() 的值為________;
的值為________;
(2)這組數據的平均數是________,眾數是________,中位數是________;
(3)根據統計的這組每天居家體育活動時間的樣本數據,估計該校500名九年級學生居家期間每天體育活動時間大于![]() 的學生人數.
的學生人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB,CD為兩個建筑物,建筑物AB的高度為60米,從建筑物AB的頂部A點測得建筑物CD的頂部C點的俯角∠EAC為30°,測得建筑物CD的底部D點的俯角∠EAD為45°,求建筑物CD的高度.

查看答案和解析>>
科目:初中數學 來源: 題型:
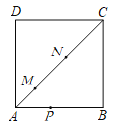
【題目】如圖,在正方形ABCD中,M、N是對角線AC上的兩個動點,P是正方形四邊上的任意一點,且![]() ,
,![]() .關于下列結論:①當△PAN是等腰三角形時,P點有6個;②當△PMN是等邊三角形時,P點有4個;③DM+DN的最小值等于6.其中,一定正確的結論的序號是_______.
.關于下列結論:①當△PAN是等腰三角形時,P點有6個;②當△PMN是等邊三角形時,P點有4個;③DM+DN的最小值等于6.其中,一定正確的結論的序號是_______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD中,點E為對角線AC上一點,且AE![]() CB,連接DE并延長交BC于點G,過點A作AH⊥BE于點H,交BC于點F.以下結論:①BH
CB,連接DE并延長交BC于點G,過點A作AH⊥BE于點H,交BC于點F.以下結論:①BH![]() HE;②∠BEG
HE;②∠BEG![]() 45°;③△ABF ≌△DCG; ④4BH2
45°;③△ABF ≌△DCG; ④4BH2![]() BG·CD.其中正確結論的個數是( )
BG·CD.其中正確結論的個數是( )
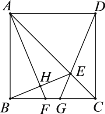
A.1個B.2
C.3D.4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC內接于⊙O,AB為⊙O的直徑,D為![]() 的中點,過D作DF⊥AB于點E,交⊙O于點F,交弦BC于點G,連接CD,BF.
的中點,過D作DF⊥AB于點E,交⊙O于點F,交弦BC于點G,連接CD,BF.
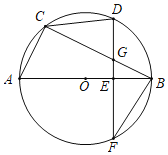
(1)求證:△BFG≌△DCG;
(2)若AC=10,BE=8,求BF的長;
(3)在(2)的條件下,P為⊙O上一點,連接BP,CP,弦CP交直徑AB于點H,若△BPH與△CPB相似,求CP的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知∠BAC=30°,把△ABC繞著點A順時針旋轉到△ADE的位置,使得點D,A,C在同一直線上.
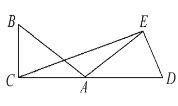
(1)△ABC旋轉了多少度?
(2)連接CE,試判斷△AEC的形狀;
(3)求 ∠AEC的度數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com