【題目】下列結論：①幾個有理數相乘，若其中負因數有奇數個，則積為負；②兩個三次多項式的和一定是三次多項式；③若xyz＜0，則
+
+
+
的值為0或﹣4；④若a，b互為相反數，則
＝﹣1；⑤若x＝y，則
＝
．其中正確的個數有（ ）
A.1個B.2個C.3個D.4個
【答案】B
【解析】
①幾個有理數相乘，如果其中一個因數為0，積為0，無論負因數的個數是奇數個還是偶數個；②兩個三次多項式的和不一定是三次多項式，也可能三次項合并后為0；③x、y、z可能兩個正數一個負數，也可能都是分數，分兩種情況求解即可得結論；④根據互為相反數的兩個數商為-1但0的相反數為0，即可判斷；⑤兩個分式的分子和分母都相同，分式的值也相同即可判斷．
解：①幾個有理數相乘，如果其中一個因數為0，積為0，所以①錯誤；
②兩個三次多項式的和不一定是三次多項式，所以②錯誤；
③∵xyz＜0，
∴分兩種情況：一種是兩正一負，設x＞0，y＞0，z＜0，
則原式=1+1-1-1=0；
一種是三個數都為負數，
則原式=-1-1-1-1=-4，所以③正確；
④∵0的相反數是0，
無意義，∴若a，b互為相反數，則＝﹣1不正確，所以④錯誤；
⑤兩個分式的分子和分母都相等，則兩個分式相等，所以⑤正確．
故選：B．
科目：初中數學 來源： 題型：
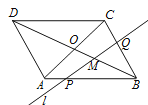
【題目】如右上圖，直線l截□ABCD的邊AB、BC和對角線BD于P、Q、M，對角線AC、BD
相交于點O，且PB＝3PA，CQ︰BQ＝1︰2，則BM︰BO＝________．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】有一個幾何體的形狀為直三棱柱，右圖是它的主視圖和左視圖．
(1)請補畫出它的俯視圖，并標出相關數據；
(2)根據圖中所標的尺寸(單位：厘米)，計算這個幾何體的全面積．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】一位農民帶上若干千克自產的土豆進城出售．為了方便，他帶了一些零錢備用，按市場價售出一些后，又降價出售，售出的土豆千克數x與他手中持有的錢數y（含備用零錢）的關系如圖所示，結合圖象回答下列問題：
（1）農民自帶的零錢是多少？
（2）求降價前農民手中的錢數y與售出的土豆千克數x的函數關系式；
（3）降價后他按每千克0.4元將剩余土豆售完，這時他手中的錢（含備用零錢）是26元，試問他一共帶了多少千克土豆？
查看答案和解析>>
科目：初中數學 來源： 題型：
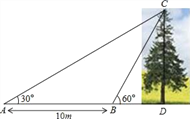
【題目】如圖，某數學興趣小組想測量一棵樹CD的高度，他們先在點A處測得樹頂C的仰角為30°，然后沿AD方向前行10m，到達B點，在B處測得樹頂C的仰角高度為60°（A、B、D三點在同一直線上）．請你根據他們測量數據計算這棵樹CD的高度（結果精確到0.1m）．（參考數據：
≈1.414，
≈1.732）
【答案】8.7米
【解析】試題分析：首先利用三角形的外角的性質求得∠ACB的度數，得到BC的長度，然后在直角△BDC中，利用三角函數即可求解．
試題解析：∵∠CBD=∠A+∠ACB，
∴∠ACB=∠CBD﹣∠A=60°﹣30°=30°，
∴∠A=∠ACB，
∴BC=AB=10（米）．
在直角△BCD中，CD=BCsin∠CBD=10×
=5≈5×1.732=8.7（米）．
答：這棵樹CD的高度為8.7米．
考點：解直角三角形的應用
【題型】解答題
【結束】
23
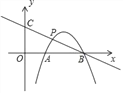
【題目】如圖，在平面直角坐標系中，拋物線y=﹣x2+ax+b交x軸于A（1，0），B（3，0）兩點，點P是拋物線上在第一象限內的一點，直線BP與y軸相交于點C．
（1）求拋物線y=﹣x2+ax+b的解析式；
（2）當點P是線段BC的中點時，求點P的坐標；
（3）在（2）的條件下，求sin∠OCB的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
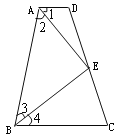
【題目】如圖，四邊形ABCD中，點E在邊CD上，連結AE、BE.給出下列五個關系式：①AD∥BC；②DE=CE；③∠1=∠2；④∠3=∠4；⑤AD＋BC=AB．將其中的三個關系式作為題設，另外兩個作為結論，構成一個命題．
⑴用序號寫出一個真命題（書寫形式如：如果×××，那么××）；并給出證明；
⑵用序號再寫出三個真命題（不要求證明）
查看答案和解析>>
科目：初中數學 來源： 題型：
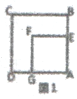
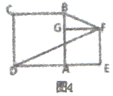
【題目】發現來源于探究。小亮進行數學探究活動，作邊長為a的正方形ABCD和邊長邊b的正方形AEFG（a>b）,開始時點E在AB上，如圖1，將正方形AEFG繞點A逆時針方向旋轉。
（1）如圖2，小亮將正方形AEFG繞點A順時針方向旋轉，連接BE、DG，請證明：△ADG≌△ABE；
（2）如圖3，小亮將正方形AEFG繞點A順時針方向旋轉，連接BE、DG，當點G恰好落在線段BE上，且a=3,b=2時，請你幫他求此時DG的長。
（3）如圖4，小亮旋轉正方形AEFG，當點E在DA的延長線上時，連接BF、DF，若FG平分∠BFD，請你幫他求a：b的值.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，P是線段AB上一點，AB＝12cm，C、D兩點分別從P、B出發以1cm/s、2cm/s的速度同時沿直線AB向左運動（C在線段AP上，D在線段BP上），運動時間為ts
（I）若C、D運動1s時，且PD＝2AC，求AP的長；
（II）若C、D運動到任一時刻時，總有PD＝2AC，AP的長度是否變化？若不變，請求出AP的長；若變化，請說明理由；
（III）在（II）的條件下，Q是直線AB上一點，且AQ﹣BQ＝PQ，求PQ的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
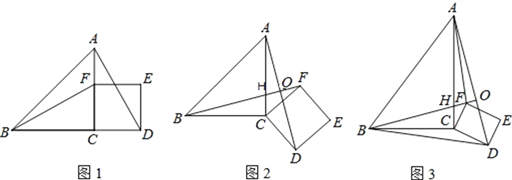
【題目】如圖1,△ABC為等腰直角三角形,∠ACB=90,F是AC邊上的一個動點(點F與A. C不重合)，以CF為一邊在等腰直角三角形外作正方形CDEF，連接BF、AD.
(1)猜想圖1中線段BF、AD的數量關系及所在直線的位置關系，直接寫出結論；
(2)將圖1中的正方形CDEF,繞著點C按順時針方向旋轉任意角度α，得到如圖2的情形。圖2中BF交AC于點H，交AD于點O，請你判斷（1）中得到的結論是否仍然成立，并證明你的判斷。
(3)將原題中的等腰直角三角形ABC改為直角三角形ABC,∠ACB=90,正方形CDEF改為矩形CDEF,如圖3,且AC=4,BC=3,CD=
,CF=1,BF交AC于點H,交AD于點O,連接BD、AF,求BD2+AF2的值。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com