
已知:關于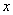 的一元二次方程
的一元二次方程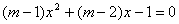 (m為實數)
(m為實數)
(1)若方程有兩個不相等的實數根,求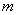 的取值范圍;
的取值范圍;
(2)在(1)的條件下,求證:無論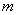 取何值,拋物線
取何值,拋物線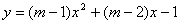 總過
總過 軸上的一個固定點;
軸上的一個固定點;
(3)若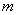 是整數,且關于
是整數,且關于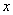 的一元二次方程
的一元二次方程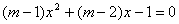 有兩個不相等的整數根,把拋物線
有兩個不相等的整數根,把拋物線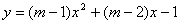 向右平移3個單位長度,求平移后的解析式.
向右平移3個單位長度,求平移后的解析式.
 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
如圖,已知一次函數y1=kx+b的圖像與x軸相交于點A,與反比例函數y2=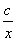 的圖像相交于B(-1,5)、C(
的圖像相交于B(-1,5)、C(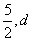 )兩點.
)兩點.
(1)求k、b的值;
(2)點P(m,n)是一次函數y1=kx+b的圖像上的動點.
寫出當-1<m≤2時,n的取值范圍;
‚設m=1-a,如果在兩個實數m與n之間(不包括m和n)有且只有一個整數,求實數a的取值范圍.

查看答案和解析>>
科目:初中數學 來源: 題型:
在平面直角坐標系中,點A、B、C的坐標分別為(2,0),(3,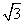 ),(1,
),(1,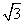 ),點D、E的坐標分別為(m,
),點D、E的坐標分別為(m,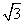 m),(n,
m),(n,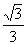 n)(m、n為非負數),則CE+DE+DB的最小值是 .
n)(m、n為非負數),則CE+DE+DB的最小值是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
已知M(a,b)是平面直角坐標系xOy中的點,其中a是從l,2,3,4三個數中任取的一個數,b是從l,2,3,4,5四個數中任取的一個數。定義“點M(a,b)在直線x+y=n上”為事件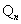 (2≤n≤9,n為整數),則當
(2≤n≤9,n為整數),則當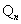 的概率最大時,n的所有可能的值為( )
的概率最大時,n的所有可能的值為( )
A.5 B.4或5 C.5或6 D.6或7
查看答案和解析>>
科目:初中數學 來源: 題型:
二次函數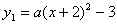 與
與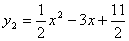 的圖像的一個交點為
的圖像的一個交點為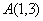 ,過點
,過點 作
作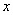 軸的平行線,分別交兩條拋物線于點
軸的平行線,分別交兩條拋物線于點 ,
,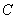 (點
(點 在點
在點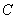 的左側) .則下列結論:(1)無論
的左側) .則下列結論:(1)無論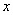 取何值,
取何值, 的值總是正數;(2)當
的值總是正數;(2)當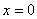 時,
時,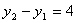 ;(3)當
;(3)當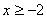 時,
時,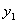 、
、 都隨
都隨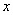 的增大而增大;(4)
的增大而增大;(4)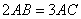 ;其中正確的是()
;其中正確的是()
A. (1) (2) B. (2) (3) C. (1) (3) (4) D. (1) (4)
查看答案和解析>>
科目:初中數學 來源: 題型:
如圖,已知平面直角坐標系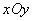 中的點
中的點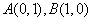 ,
,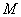 、
、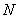 為線段
為線段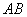 上兩動點,過點
上兩動點,過點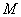 作
作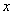 軸的平行線交
軸的平行線交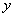 軸于點
軸于點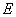 ,過點
,過點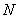 作
作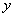 軸的平行線交
軸的平行線交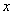 軸于點
軸于點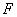 ,交直線
,交直線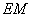 于點
于點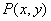 ,且
,且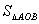 =
=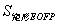 .
.
(1)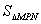
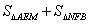 (填“>”、“=”、“<”),
(填“>”、“=”、“<”),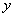 與
與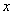 的函數關系是 (不要求寫自變量的取值范圍);
的函數關系是 (不要求寫自變量的取值范圍);
(2)當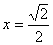 時,求
時,求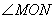 的度數;
的度數;
(3)證明: 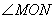 的度數為定值.
的度數為定值.
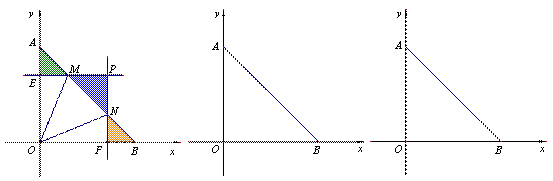
( 備用圖) (備用圖)
| |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com