
(12分)在平面直角坐標系中,O為坐標原點,點A坐標為(1,0),以OA為邊在第一象限內作等邊△OAB,C為x軸正半軸上的一個動點(OC>1),連接BC,以BC為邊在第一象限內作等邊△BCD,直線DA交y軸于E點.

(1)如圖,當C點在x軸上運動時,設AC=x,請用x表示線段AD的長;
(2)隨著C點的變化,直線AE的位置變化嗎?若變化,請說明理由;若不變,請求出直線AE的解析式.
(3)以線段BC為直徑作圓,圓心為點F,
①當C點運動到何處時直線EF∥直線BO?此時⊙F和直線BO的位置關系如何?請說明理由.
②G為CD與⊙F的交點,H為直線DF上的一個動點,連結HG、HC,求HG+HC的最小值,并將此最小值用x表示.
(1)AD=1+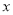 (2)y=
(2)y=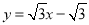 (3)
(3)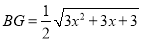
【解析】
試題分析:(1)由△OAB和△BCD都為等邊三角形,等邊三角形的邊長相等,且每一個內角都為60°,得到∠OBA=∠DBC,等號兩邊都加上∠ABC,得到∠OBC=∠ABD,根據“SAS”得到△OBC≌△ABD,即可得到對應邊AD與OC相等,由OC表示出AD即可;
(2)隨著C點的變化,直線AE的位置不變.理由為:由(1)得到的兩三角形全等,得到∠BAD=∠BOC=60°,又等邊三角形BCD,得到∠BAO=60°,根據平角定義及對頂角相等得到∠OAE=60°,在直角三角形OAE中,由OA的長,根據tan60°的定義求出OE的長,確定出點E的坐標,設出直線AE的方程,把點A和E的坐標代入即可確定出解析式;
(3)①由EA與OB平行,且EF也與OB平行,根據過直線外一點作已知直線的平行線有且只有一條,得到EF與EA重合,所以F為BC與AE的交點,又F為BC的中點,得到A為OC中點,由A的坐標即可求出C的坐標;相切,理由是由F為等邊三角形BC邊的中點,根據“三線合一”得到DF與BC垂直,由EF與OB平行得到BF與OB垂直,得證;
②根據等邊三角形的“三線合一”得到DF垂直平分BC,所以C與D關于DF對稱,所以GB為HC+HG的最小值,GB的求法是:由B,C及G三點在圓F圓周上,得到FB,FC及FG相等,利用一邊的中線等于這邊的一半得到三角形BCG為直角三角形,根據“三線合一”得到∠CBG為30°,利用cos30°和BC的長即可求出BG,而BC的長需要過B作BM垂直于x軸,根據等邊三角形的性質求出BM及AM,表示出CM,在直角三角形BMC中,根據勾股定理表示出BC的長即可..
考點:1.一次函數綜合題;2.等邊三角形的性質;3.直線與圓的位置關系;4.軸對稱-最短路線問題.


 通城學典默寫能手系列答案
通城學典默寫能手系列答案 金牌教輔培優優選卷期末沖刺100分系列答案
金牌教輔培優優選卷期末沖刺100分系列答案科目:初中數學 來源:2014-2015學年江蘇省丹陽市八年級上學期期中考試數學試卷(解析版) 題型:填空題
若直角三角形斜邊上的高和中線長分別是4cm,5cm,則它的面積是 cm2.
查看答案和解析>>
科目:初中數學 來源:2014-2015學年江蘇省丹陽市八年級上學期期中考試數學試卷(解析版) 題型:選擇題
如果等腰三角形的兩邊長為3cm、6cm,那么它的周長為( )
A.9cm B.12cm或15cm C.12cm D.15cm
查看答案和解析>>
科目:初中數學 來源:2014-2015學年江蘇省東臺市九年級上學期期中考試數學試卷(解析版) 題型:解答題
(9分)甲、乙兩個小組各10名同學進行英語口語會話練習,各練習5次,他們每個同學合格的次數分別如下:
甲組:4,1,2,2,1,3,3,1,2,1。
乙組:4,3,0,2,1,3,3,0,1,3。
(1).如果合格3次以上(含3次)作為及格標準,請你說明哪個小組的及格率高?
(2).試計算兩個小組的方差,請你比較哪個小組的口語會話的合格次數比較穩定?
查看答案和解析>>
科目:初中數學 來源:2014-2015學年江蘇省東臺市九年級上學期期中考試數學試卷(解析版) 題型:填空題
如圖,一圓與平面直角坐標系中的x軸切于點A(8,0),與y軸交于點B(0,4),C(0,16),則該圓的直徑為_________.
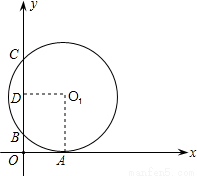
查看答案和解析>>
科目:初中數學 來源:2014-2015學年江蘇省東臺市九年級上學期期中考試數學試卷(解析版) 題型:解答題
(12分)已知直線l與⊙O,AB是⊙O的直徑,AD⊥l于點D.

(1)如圖①,當直線l與⊙O相切于點C時,若∠DAC=30°,求∠BAC的大小;
(2)如圖②,當直線l與⊙O相交于點E、F時,若∠DAE=18°,求∠BAF的大小.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com