
【題目】如圖,在![]() 中,已知
中,已知![]() ,
,![]() ,
,![]() 是
是![]() 的高,
的高,![]() ,
,![]() ,直線
,直線![]() ,動點
,動點![]() 從點
從點![]() 開始沿射線
開始沿射線![]() 方向以每秒
方向以每秒![]() 厘米的速度運動,動點
厘米的速度運動,動點![]() 也同時從點
也同時從點![]() 開始在直線
開始在直線![]() 上以每秒
上以每秒![]() 厘米的速度向遠離
厘米的速度向遠離![]() 點的方向運動,連接
點的方向運動,連接![]() 、
、![]() ,設(shè)運動時間為
,設(shè)運動時間為![]() 秒.
秒.

(1)請直接寫出![]() 、
、![]() 的長度(用含有
的長度(用含有![]() 的代數(shù)式表示):
的代數(shù)式表示):![]() ______
______![]() ,
,![]() ______
______![]() ;
;
(2)當![]() 為多少時,
為多少時,![]() 的面積為
的面積為![]() ?
?
(3)請利用備用圖探究,當![]() ___________秒時,
___________秒時,![]() .
.
【答案】(1)![]() ,
,![]() ;(2)當
;(2)當![]() 為
為![]() 或
或![]() 時,
時,![]() 的面積為
的面積為![]() ;(3)
;(3)![]() .
.
【解析】
(1)根據(jù)“![]() ”即可得;
”即可得;
(2)根據(jù)![]() 可求出BD的長,因為要求t則需要求出CD的長,由點D的位置可知,需分點D在點B右側(cè)和點D在點B左側(cè)兩種情況,根據(jù)線段的和與差分別討論即可;
可求出BD的長,因為要求t則需要求出CD的長,由點D的位置可知,需分點D在點B右側(cè)和點D在點B左側(cè)兩種情況,根據(jù)線段的和與差分別討論即可;
(3)先假設(shè)![]() ,則有
,則有![]() ,同題(2)分兩種情況討論解出t的值,再檢驗兩種情況下的t值,能否使得
,同題(2)分兩種情況討論解出t的值,再檢驗兩種情況下的t值,能否使得![]() ,把不符合的舍去即可.
,把不符合的舍去即可.
(1)由“![]() ”得:
”得:![]()
故答案為:![]() ;
;
(2)![]() ,
,![]()
![]() ,為求CD的長分以下兩種情況:
,為求CD的長分以下兩種情況:
若![]() 在
在![]() 點右側(cè),
點右側(cè),![]() ,則
,則![]()
若![]() 在
在![]() 點左側(cè),
點左側(cè),![]() ,則
,則![]()
綜上所述:當![]() 為
為![]() 或
或![]() 時,
時,![]() 的面積為
的面積為![]() ;
;
(3)如果![]() ,則有
,則有![]()
同題(2)分兩種情況:
①若![]() 在
在![]() 點右側(cè),則
點右側(cè),則![]()
由![]() ,即
,即![]() 可得:
可得:![]()
檢驗:![]()
![]()
![]()
![]()
![]()
因此,由![]() 定理可得
定理可得![]()
②若![]() 在
在![]() 點左側(cè),則
點左側(cè),則![]()
由![]() ,即
,即![]() 可得:
可得:![]()
檢驗:![]()
![]()
![]()
![]()
![]()
![]()
因此,![]() 推不出
推不出![]()
綜上,![]() 秒時,
秒時,![]() .
.


科目:初中數(shù)學 來源: 題型:
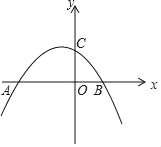
【題目】如圖,已知拋物線y=﹣![]() x2+bx+c與x軸交于點A(﹣4,0),B(2,0),與y軸交于點C.請解答下列問題:
x2+bx+c與x軸交于點A(﹣4,0),B(2,0),與y軸交于點C.請解答下列問題:
(1)求拋物線的函數(shù)解析式并直接寫出頂點M坐標;
(2)連接AM,N是AM的中點,連接BN,求線段BN長.
注:拋物線y=ax2+bx+c(a≠0)的頂點坐標是(﹣![]() ,
,![]() ).
).
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】(觀察)
51×49=(![]() )2﹣(
)2﹣(![]() )2
)2
102×98=(![]() )2﹣(
)2﹣(![]() )2
)2
2001×1999=(![]() )2﹣(
)2﹣(![]() )2
)2
(發(fā)現(xiàn))根據(jù)閱讀回答問題
(1)請根據(jù)上面式子的規(guī)律填空:
998×1002= 2﹣ 2
(2)在上述乘法運算中,設(shè)第一個因數(shù)為m,第二個因數(shù)為n,請用有m、n的符號語言寫出你所發(fā)現(xiàn)的規(guī)律,并證明.
(應用)請運用(發(fā)現(xiàn))中總結(jié)的規(guī)律計算:59.8×60.2
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】已知二次函數(shù)y=2x2﹣4x﹣6.
(1)求這個二次函數(shù)圖象的頂點坐標及對稱軸;
(2)指出該圖象可以看作拋物線y=2x2通過怎樣平移得到?
(3)在給定的坐標系內(nèi)畫出該函數(shù)的圖象,并根據(jù)圖象回答:當x取多少時,y隨x增大而減小;當x取多少時,y<0.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
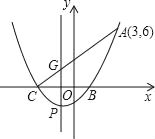
【題目】如圖,一元二次方程x2+2x﹣3=0的兩根x1,x2(x1<x2)是拋物線y=ax2+bx+c與x軸的兩個交點C,B的橫坐標,且此拋物線過點A(3,6).
(1)求此二次函數(shù)的解析式;
(2)設(shè)此拋物線的頂點為P,對稱軸與線段AC相交于點G,則P點坐標為 ,G點坐標為 ;
(3)在x軸上有一動點M,當MG+MA取得最小值時,求點M的坐標.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,在等邊△ABC中,D、E分別是BC、AC上的動點且BD=CE,連接AD與BE相交于點F,連接CF,下列結(jié)論:①△ABD≌△BCE;②∠AFB=120°;③若BD=CD,則FA=FB=FC;④∠AFC=90°,則AF=3BF,其中正確的結(jié)論共有( )

A.1個B.2個C.3個D.4個
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】已知:y-2與x3成正比例,且x=4時y=8.
(1)求y與x之間的函數(shù)關(guān)系式;
(2)當y=-6時,求x的值.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】平面直角坐標系xOy中,橫坐標為a的點A在反比例函數(shù)y1═![]() (x>0)的圖象上,點A′與點A關(guān)于點O對稱,一次函數(shù)y2=mx+n的圖象經(jīng)過點A′.
(x>0)的圖象上,點A′與點A關(guān)于點O對稱,一次函數(shù)y2=mx+n的圖象經(jīng)過點A′.
(1)設(shè)a=2,點B(4,2)在函數(shù)y1、y2的圖象上.
①分別求函數(shù)y1、y2的表達式;
②直接寫出使y1>y2>0成立的x的范圍;
(2)如圖①,設(shè)函數(shù)y1、y2的圖象相交于點B,點B的橫坐標為3a,△AA'B的面積為16,求k的值;
(3)設(shè)m=![]() ,如圖②,過點A作AD⊥x軸,與函數(shù)y2的圖象相交于點D,以AD為一邊向右側(cè)作正方形ADEF,試說明函數(shù)y2的圖象與線段EF的交點P一定在函數(shù)y1的圖象上.
,如圖②,過點A作AD⊥x軸,與函數(shù)y2的圖象相交于點D,以AD為一邊向右側(cè)作正方形ADEF,試說明函數(shù)y2的圖象與線段EF的交點P一定在函數(shù)y1的圖象上.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】在學校組織的“文明出行”知識競賽中,8(1)和8(2)班參賽人數(shù)相同,成績分為A、B、C三個等級,其中相應等級的得分依次記為A級100分、B級90分、C級80分,達到B級以上(含B級)為優(yōu)秀,其中8(2)班有2人達到A級,將兩個班的成績整理并繪制成如下的統(tǒng)計圖,請解答下列問題:

(1)求各班參賽人數(shù),并補全條形統(tǒng)計圖;
(2)此次競賽中8(2)班成績?yōu)?/span>C級的人數(shù)為_______人;
(3)小明同學根據(jù)以上信息制作了如下統(tǒng)計表:
平均數(shù)(分) | 中位數(shù)(分) | 方差 | |
8(1)班 | m | 90 | n |
8(2)班 | 91 | 90 | 29 |
請分別求出m和n的值,并從優(yōu)秀率和穩(wěn)定性方面比較兩個班的成績;
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com