
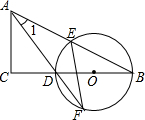
 如圖,△ABC中,∠C=90°,D是BC邊上一點,以DB為直徑的⊙O交AB于E,交AD的延長線于F,連結EF,∠1=∠F.
如圖,△ABC中,∠C=90°,D是BC邊上一點,以DB為直徑的⊙O交AB于E,交AD的延長線于F,連結EF,∠1=∠F.分析 (1)連接DE,由BD是⊙O的直徑,得到∠DEB=90°,由于E是AB的中點,得到DA=DB,根據(jù)等腰三角形的性質得到∠1=∠B等量代換即可得到結論;
(2)根據(jù)等腰三角形的判定定理得到AE=EF=4$\sqrt{5}$,推出AB=2AE=8$\sqrt{5}$,在Rt△ABC中,根據(jù)勾股定理得到BC,設CD=x,根據(jù)勾股定理列方程即可得到結論.
解答 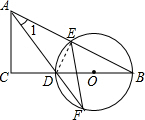 解:(1)證明:連接DE,
解:(1)證明:連接DE,
∵BD是⊙O的直徑,
∴∠DEB=90°,
∵E是AB的中點,
∴DA=DB,
∴∠1=∠B,
∵∠B=∠F,
∴∠1=∠F;
(2)∵∠1=∠F,
∴AE=EF=4$\sqrt{5}$,
∴AB=2AE=8$\sqrt{5}$,
在Rt△ABC中,∵tanB=$\frac{1}{2}$,
∴BC=2AC,∴BC=16,
設CD=x,則AD=BD=16-x,
∵AC2+CD2=AD2,
即82+x2=(16-x)2,
∴x=3
6,即CD=6.
點評 本題考查了圓周角定理,解直角三角形的性質,等腰三角形的性質,勾股定理,正確的作出輔助線構造直角三角形是解題的關鍵.


科目:初中數(shù)學 來源: 題型:選擇題
| A. | -a+b+c+d=-(a-b)-(-c-d) | B. | x-(y-z)=x-y-z | ||
| C. | x+2y-2z=x-2(z+y) | D. | -(x-y+z)=-x-y-z |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
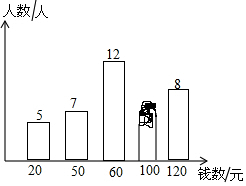 小明調查了學校50名同學本學期購買課外書的花費情況,并將結果繪制成了下面的統(tǒng)計圖,由于不小心滴上了墨水,導致花費為100元的人數(shù)看不清楚了.求出這50名學生本學期購買課外書花費的眾數(shù)、中位數(shù)和平均數(shù).
小明調查了學校50名同學本學期購買課外書的花費情況,并將結果繪制成了下面的統(tǒng)計圖,由于不小心滴上了墨水,導致花費為100元的人數(shù)看不清楚了.求出這50名學生本學期購買課外書花費的眾數(shù)、中位數(shù)和平均數(shù).查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
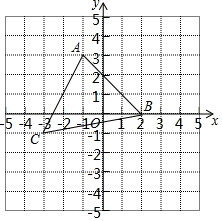 如圖,在平面直角坐標系中有一個△ABC,頂點A(-1,3),B(2,0),C(-3,-1).
如圖,在平面直角坐標系中有一個△ABC,頂點A(-1,3),B(2,0),C(-3,-1).查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
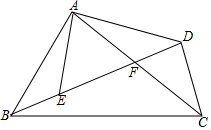 如圖,在四邊形ABCD中,AC、BD相交于點F,點E在BD上,且$\frac{AB}{AE}$=$\frac{BC}{ED}$=$\frac{AC}{AD}$.
如圖,在四邊形ABCD中,AC、BD相交于點F,點E在BD上,且$\frac{AB}{AE}$=$\frac{BC}{ED}$=$\frac{AC}{AD}$.查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com