【題目】如圖1，已知AB=AC，D為∠BAC的角平分線上面一點，連接BD，CD；如圖2，已知AB=AC，D、E為∠BAC的角平分線上面兩點，連接BD，CD，BE，CE；如圖3，已知AB=AC，D、E、F為∠BAC的角平分線上面三點，連接BD，CD，BE，CE，BF，CF；…，依次規(guī)律，第12個圖形中有全等三角形的對數(shù)是( )
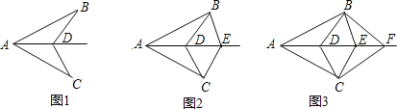
A. 80對B. 78對C. 76對D. 以上都不對
千里馬走向假期期末仿真試卷寒假系列答案科目：初中數(shù)學(xué) 來源： 題型：
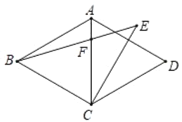
【題目】如圖，在菱形ABCD中，∠BAD＝120°，CE⊥AD，且CE＝BC，連接BE交對角線AC于點F，則∠EFC＝_____°．
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
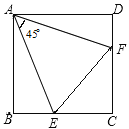
【題目】如圖，在正方形ABCD中，點E在BC上，點F在CD上，連接AE、AF、EF，∠EAF=45°，BE=3，CF=4，則正方形的邊長為__________．
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
【題目】如圖，正方形ABCD與正方形A1B1C1D1關(guān)于某點中心對稱，已知A, D1,D三點的坐標(biāo)分別是（0,4），（0，3），（0，2）.
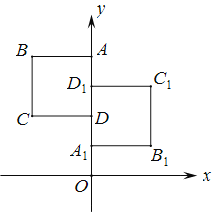
(1)對稱中心的坐標(biāo)；
(2)寫出頂點B, C, B1 , C1的坐標(biāo).
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
【題目】操作：在△ABC中，AC＝BC＝2，∠C＝90°，將一塊等腰三角形板的直角頂點放在斜邊AB的中點P處，將三角板繞點P旋轉(zhuǎn)，三角板的兩直角邊分別交射線AC、CB于D、E兩點。圖①，②，③是旋轉(zhuǎn)三角板得到的圖形中的3種情況。研究：
（1）三角板ABC繞點P旋轉(zhuǎn)，觀察線段PD和PE之間有什么數(shù)量關(guān)系？并結(jié)合圖②加以證明。
（2）三角板ABC繞點P旋轉(zhuǎn)，△PBE是否能為等腰三角形？若能，指出所有情況（即寫出△PBE為等腰三角形時CE的長）；若不能，請說明理由。（圖④不用）
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
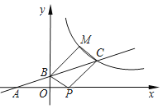
【題目】如圖所示，直線
與
軸交于點
，與
軸交于點
，與反比例函
的圖象交于點
，且
．
（1）求點的坐標(biāo)和反比例函數(shù)
的解析式；
（2）點
在軸上，反比例函數(shù)圖象上存在點
，使得四邊形
為平行四邊形，求點M的坐標(biāo)．
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
【題目】公元前5世紀(jì)，畢達(dá)哥拉斯學(xué)派中的一名成員希伯索斯發(fā)現(xiàn)了無理數(shù)
，導(dǎo)致了第一次數(shù)學(xué)危機(jī).是無理數(shù)的證明如下：
假設(shè)是有理數(shù)，那么它可以表示成
（
與
是互質(zhì)的兩個正整數(shù)）.于是
，所以，
.于是
是偶數(shù)，進(jìn)而是偶數(shù).從而可設(shè)
，所以
，
，于是可得也是偶數(shù).這與“與是互質(zhì)的兩個正整數(shù)”矛盾，從而可知“是有理數(shù)”的假設(shè)不成立，所以，是無理數(shù).這種證明“是無理數(shù)”的方法是( )
A.綜合法B.反證法C.舉反例法D.數(shù)學(xué)歸納法
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
【題目】如圖，△ABC中，AC=BC，CE為△ABC的中線，BD為AC邊上的高，BF平分∠CBD交CE于點G，連接AG交BD于點M，若∠AFG=63°，則∠AMB的度數(shù)為________.
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
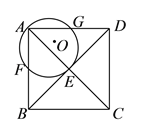
【題目】如圖，在正方形
中， 
為對角線
， 
的交點，經(jīng)過點
和點
作⊙
，分別交
， 
于點
， 
．已知正方形邊長為
，⊙
的半徑為
，則
的值為__________．
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
