
 已知邊長(zhǎng)為6的等邊三角形ABC,兩頂點(diǎn)A、B分別在直角墻面上滑動(dòng),連接OC,則OC的長(zhǎng)的最大值是
已知邊長(zhǎng)為6的等邊三角形ABC,兩頂點(diǎn)A、B分別在直角墻面上滑動(dòng),連接OC,則OC的長(zhǎng)的最大值是| 3 |
| 3 |

| 1 |
| 2 |
| 62-32 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |


 閱讀快車系列答案
閱讀快車系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
 (2013•黑龍江)已知等邊三角形ABC的邊長(zhǎng)是2,以BC邊上的高AB1為邊作等邊三角形,得到第一個(gè)等邊三角形AB1C1,再以等邊三角形AB1C1的B1C1邊上的高AB2為邊作等邊三角形,得到第二個(gè)等邊三角形AB2C2,再以等邊三角形AB2C2的邊B2C2邊上的高AB3為邊作等邊三角形,得到第三個(gè)等邊AB3C3;…,如此下去,這樣得到的第n個(gè)等邊三角形ABnCn的面積為
(2013•黑龍江)已知等邊三角形ABC的邊長(zhǎng)是2,以BC邊上的高AB1為邊作等邊三角形,得到第一個(gè)等邊三角形AB1C1,再以等邊三角形AB1C1的B1C1邊上的高AB2為邊作等邊三角形,得到第二個(gè)等邊三角形AB2C2,再以等邊三角形AB2C2的邊B2C2邊上的高AB3為邊作等邊三角形,得到第三個(gè)等邊AB3C3;…,如此下去,這樣得到的第n個(gè)等邊三角形ABnCn的面積為| 3 |
| 3 |
| 4 |
| 3 |
| 3 |
| 4 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
| EG |
| FH |
| b |
| a |
| EG |
| FH |
| b |
| a |
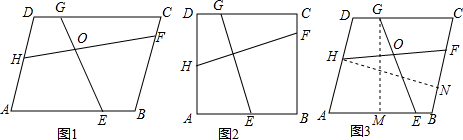
查看答案和解析>>
科目:初中數(shù)學(xué) 來源:2013年初中畢業(yè)升學(xué)考試(黑龍江龍東地區(qū)卷)數(shù)學(xué)(解析版) 題型:填空題
已知等邊三角形ABC的邊長(zhǎng)是2,以BC邊上的高AB1為邊作等邊三角形,得到第一個(gè)等邊三角形AB1C1,再以等邊三角形AB1C1的B1C1邊上的高AB2為邊作等邊三角形,得到第二個(gè)等邊三角形AB2C2,再以等邊三角形AB2C2的邊B2C2邊上的高AB3為邊作等邊三角形,得到第三個(gè)等邊AB3C3;…,如此下去,這樣得到的第n個(gè)等邊三角形ABnCn的面積為 .

查看答案和解析>>
科目:初中數(shù)學(xué) 來源:2013年黑龍江省龍東地區(qū)中考數(shù)學(xué)試卷(解析版) 題型:填空題

查看答案和解析>>
科目:初中數(shù)學(xué) 來源:2009年廣西玉林市北流市新豐初中中考數(shù)學(xué)一模試卷(解析版) 題型:解答題
 ,可得
,可得 .
.
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com