
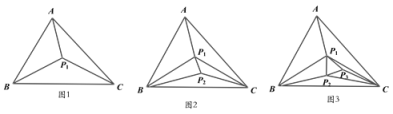
【題目】(問題背景)在△ABC內部,有地點![]() ,可構成3個不重疊的小三角形(如圖1)
,可構成3個不重疊的小三角形(如圖1)
(探究發現)當△ABC內的點的個數增加時,若其他條件不變,探究三角形內互不重疊的小三角形的個數情況。
(1)填表:
三角形內點的個數n | 1 | 2 | 3 | 4 | …… |
不重疊三角形個數S | …… |
(2)當△ABC內部有2019個點(![]() ,
,![]() ……
……![]() )時,三角形內不重疊的小三角形的個數S為多少?
)時,三角形內不重疊的小三角形的個數S為多少?
【答案】(1)3,5,7,9;
(2)4039.
【解析】
根據前三個探究不難發現,三角形內部每增加一個點,不重疊的小三角形的個數增加2個,根據此規律寫出當△ABC內部有m個點時,三角形內不重疊的小三角形的個數為3+2(m-1),然后計算即可.
(1)當△ABC內部有1個點時,三角形內不重疊的小三角形的個數為:3=3+2(1-1),
當△ABC內部有2個點時,三角形內不重疊的小三角形的個數為:5=3+2(2-1),
當△ABC內部有3個點時,三角形內不重疊的小三角形的個數為:7=3+2(3-1),
當△ABC內部有4個點時,三角形內不重疊的小三角形的個數為:9=3+2(4-1),
…,
所以,當△ABC內部有m個點時,三角形內不重疊的小三角形的個數為:3+2(m-1).
故表中應依次填:3,5,7,9;
(2)由(1)可得:當m=2019時,3+2×(2019-1)=4039(個),
答:當△ABC內部有2019個點(P1,P2……P2019)時,三角形內不重疊的小三角形的個數S為4039.


 名師點撥卷系列答案
名師點撥卷系列答案 英才計劃期末調研系列答案
英才計劃期末調研系列答案科目:初中數學 來源: 題型:
【題目】我市智慧閱讀活動正如火如茶地進行.某班學習委員為了解11月份全班同學課外閱讀的情況,調查了全班同學11月份讀書的冊數,并根據調查結果繪制了如下不完整的條形統計圖和扇形統計圖:
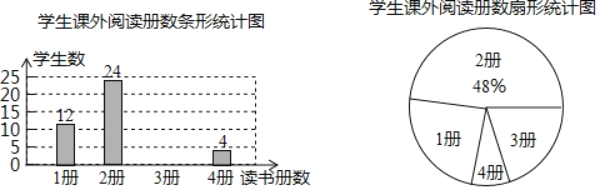
(1)扇形統計圖中“3冊”部分所對應的圓心角的度數是 ,并把條形統計圖補充完整;
(2)該班的學習委員11月份的讀書冊數為4冊,若該班的班主任從11月份讀書4冊的學生中隨機抽取兩名同學參加學校舉行的知識競賽,請用列表法或畫樹狀圖求恰好有一名同學是學習委員的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】問題探究
(1)如圖1,△ABC和△DEC均為等腰直角三角形,且∠BAC=∠CDE=90°,AB=AC=3,DE=CD=1,連接AD、BE,求![]() 的值;
的值;
(2)如圖2,在Rt△ABC中,∠ACB=90°,∠B=30°,BC=4,過點A作AM⊥AB,點P是射線AM上一動點,連接CP,做CQ⊥CP交線段AB于點Q,連接PQ,求PQ的最小值;

(3)李師傅準備加工一個四邊形零件,如圖3,這個零件的示意圖為四邊形ABCD,要求BC=4cm,∠BAD=135°,∠ADC=90°,AD=CD,請你幫李師傅求出這個零件的對角線BD的最大值。
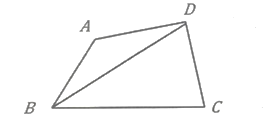
圖3
查看答案和解析>>
科目:初中數學 來源: 題型:
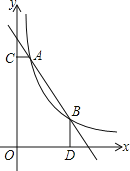
【題目】如圖,一次函數![]() 與函數
與函數![]() 的圖象交于
的圖象交于![]() ,
,![]() 兩點,
兩點,![]() 軸于C,
軸于C,![]() 軸于D
軸于D
![]() 求k的值;
求k的值;
![]() 根據圖象直接寫出
根據圖象直接寫出![]() 的x的取值范圍;
的x的取值范圍;
![]() 是線段AB上的一點,連接PC,PD,若
是線段AB上的一點,連接PC,PD,若![]() 和
和![]() 面積相等,求點P坐標.
面積相等,求點P坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】《九章算術》中記載:“今有共買羊,人出五,不足四十五;人出七,不足三,問人數、價價各幾何?“其大意是:今有人合伙買羊,若每人出5錢,還差45錢;若每人出7錢,還差3錢,問:合伙人數、羊價各是多少?設合伙人數為![]() 人,羊價為
人,羊價為![]() 錢,根據題意,可列方程組( )
錢,根據題意,可列方程組( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
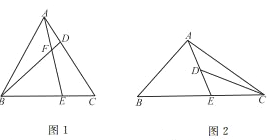
【題目】如圖1,在△ABC中,D,E分別是AC,BC邊上的點,且AD=CE,連接BD,AE相交于點F。
(1)當∠ABC=∠C=60°時,![]() ,那么
,那么![]() ;(直接寫出結論)
;(直接寫出結論)
(2)當△ABC為等邊三角形,![]() 時,請用含n的式子表示AF,BF的數量關系,并說明理由;
時,請用含n的式子表示AF,BF的數量關系,并說明理由;
(3)如圖2,在△ABC中,∠ABC=45°,∠ACB=30°,AC=![]() ,點E在BC上,點D是AE的中點,當∠EDC=30°時,CE和DE的數量關系為。(直接寫出結論,不必證明)
,點E在BC上,點D是AE的中點,當∠EDC=30°時,CE和DE的數量關系為。(直接寫出結論,不必證明)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,D是AB邊的中點,E是AC邊上一點,聯結DE,過點D作
,D是AB邊的中點,E是AC邊上一點,聯結DE,過點D作![]() 交BC邊于點F,聯結EF.
交BC邊于點F,聯結EF.
(1)如圖1,當![]() 時,求EF的長;
時,求EF的長;
(2)如圖2,當點E在AC邊上移動時, ![]() 的正切值是否會發生變化,如果變化請說出變化情況;如果保持不變,請求出
的正切值是否會發生變化,如果變化請說出變化情況;如果保持不變,請求出![]() 的正切值;
的正切值;
(3)如圖3,聯結CD交EF于點Q,當![]() 是等腰三角形時,請直接寫出BF的長.
是等腰三角形時,請直接寫出BF的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=ax2+bx﹣3a經過點A(﹣1,0)、C(0,3),與x軸交于另一點B,拋物線的頂點為D.

(1)求此二次函數解析式;
(2)連接DC、BC、DB,求證:△BCD是直角三角形;
(3)在對稱軸右側的拋物線上是否存在點P,使得△PDC為等腰三角形?若存在,求出符合條件的點P的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
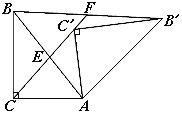
【題目】如圖,Rt△ABC中,∠ACB=90°,Rt△AB′C′是由Rt△ABC繞點A順時針旋轉得到的,連接CC′交斜邊于點E,CC′的延長線交BB′于點F.
(1)證明:△AC C′∽△AB B′;
(2)設∠ABC=α,∠CAC′=β,試探索α、β滿足什么關系時AC=BF,并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com