
【題目】已知∠MON = 50°,OE 平分∠MON,點A、B、C分別是射線OM、OE、ON上的動點(A、B、C不與點O重合),連接AC交射線OE于點D、設∠OAC = x°.
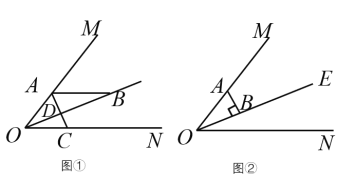
(1)如圖①,若AB//ON,
①則∠ABO 的度數是________;
②當∠BAD =∠ABD 時,x=_______;當∠BAD = ∠BDA 時,x=________.
(2)如圖②,若AB⊥OE,則是否存在這樣的x值,使得 △ABD 中有一個角是另一個角的兩倍.存在,直接寫出x的值;不存在,說明理由.
【答案】(1)①25°,②105,52.5;(2)存在,x的值為20,110,5,125,35,95.
【解析】
(1)利用角平分線的性質求出∠ABO的度數是關鍵,利用三角形的內角和定理及其推論計算求解即可.
(2)按點D在線段OB上或OB的延長線上分兩大類,再根據△ABD 中有一個角是另一個角的兩倍的三種可能性再分類,利用三角形的內角和及其推論分別求解計算即可.
解:(1)①∵∠MON=50°,OE平分∠MON∴∠AOB=∠BON=25°
∵AB∥ON∴∠ABO=25°
②當∠BAD=∠ABD,則∠BAD=25°
∵∠AOB+∠ABO+∠OAB=180°
∴∠AOB+∠ABO+∠OAC+∠BAD=180°
∴∠OAC=180°-∠AOB-∠ABO-∠BAD =180°-25°-25°-25°=105°
當∠BAD=∠BDA,∵∠ABO=25°
∴∠BAD=77.5°
∵∠AOB+∠ABO+∠OAB=180°
∴∠OAB=180°-∠ABO-∠AOB=180°-25°-25°=130°
∴∠OAC=∠OAB-∠BAD=130°-77.5°=52.5°
故答案為:①25°;②105,52.5;
(2)存在,推導如下
當點D在線段OB上時,如圖③所示:
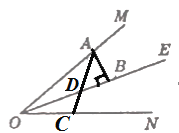
圖③
i)當∠ABD=2∠DAB=90°時,則∠ADB=∠DAB=45°,
∵∠AOD+∠OAC=∠ADB,
∴∠OAC=∠ADB-∠AOD=45°-25°=20°,
ii)當∠ADB=2∠DAB時,∵∠ABD=90°,∴∠ADB=60°,
∵∠AOD+∠OAC=∠ADB,
∴∠OAC=∠ADB-∠AOD=60°-25°=35°,
iii) 當∠DAB=2∠ADB時, ∵∠ABD=90°,∴∠ADB=30°,
∵∠AOD+∠OAC=∠ADB,
∴∠OAC=∠ADB-∠AOD=30°-25°=5°.
當點D在線段OB延長線上時,如圖③所示:

圖③
i)當∠ABD=2∠DAB=90°時,則∠ADB=∠DAB=45°,
∵∠AOD+∠OAC+∠ADB=180°,
∴∠OAC=180°-∠AOD-∠ADB=180°-25°-45°=110°;
ii)當∠ADB=2∠DAB時,∵∠ABD=90°,∴∠ADB=60°,
∵∠AOD+∠OAC+∠ADB=180°,
∴∠OAC=180°-∠AOD-∠ADB=180°-25°-60°=95°;
iii) 當∠DAB=2∠ADB時, ∵∠ABD=90°,∴∠ADB=30°,
∵∠AOD+∠OAC+∠ADB=180°,
∴∠OAC=180°-∠AOD-∠ADB=180°-25°-30°=125°;
綜上所述,存在這樣的∠OAC,使得 △ABD 中有一個角是另一個角的兩倍,其值x
為20,110,5,125,35,95.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,菱形OACB的頂點O在原點,點C的坐標為(4,0),點B的縱坐標是﹣1,則頂點A坐標是( )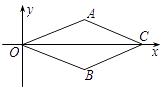
A.(2,1)
B.(1,﹣2)
C.(1,2)
D.(2,﹣1)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:點E為AB邊上的一個動點.
(1)如圖1,若△ABC是等邊三角形,以CE為邊在BC的同側作等邊△DEC,連結AD.試比較∠DAC與∠B的大小,并說明理由;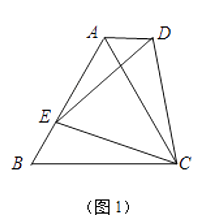
(2)如圖2,若△ABC中,AB=AC,以CE為底邊在BC的同側作等腰△DEC,且△DEC∽△ABC,連結AD.試判斷AD與BC的位置關系,并說明理由;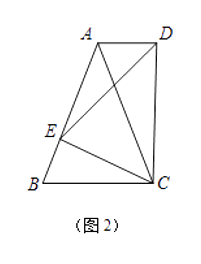
(3)如圖3,若四邊形ABCD是邊長為2的正方形,以CE為邊在BC的同側作正方形ECGF.
①試說明點G一定在AD的延長線上;
②當點E在AB邊上由點B運動至點A時,點F隨之運動,求點F的運動路徑長.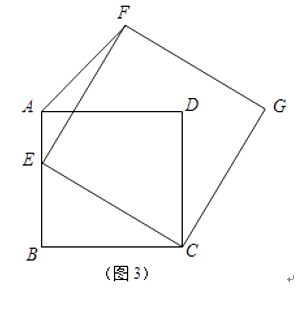
查看答案和解析>>
科目:初中數學 來源: 題型:
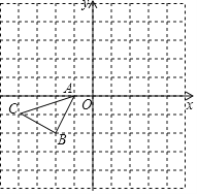
【題目】如圖,方格紙中的每個小正方形的邊長都為1,在建立平面直角坐標系后,△ABC的頂點均在格點上.
(1)以點A為旋轉中心,將△ABC繞點A順時針旋轉90°得到△AB1C1,畫出△AB1C1;
(2)畫出△ABC關于原點O成中心對稱的△A2B2C2,若點B的坐標為(-2,-2),則點B2的坐標為_________.
(3)若△A2B2C2可看作是由△AB1C1繞點P順時針旋轉90°得到的,則點P的坐標為______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,A、B兩個碼頭分別在一條河的兩岸AC、BD上,河岸AC、BD均為東西走向,一艘客輪以每小時30千米的速度由A碼頭出發沿北偏東50°的方向航行至B碼頭,用時1.2小時,求該河的寬度(結果精確到1千米)
【參考數據:sin50°=0.77,cos50°=0.64,tan50°=1.20】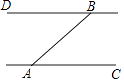
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AE平分∠BAC,BE⊥AE于點E,點F是BC的中點.
(1)如圖1,BE的延長線與AC邊相交于點D,求證:EF=![]() (AC﹣AB);
(AC﹣AB);
(2)如圖2,請直接寫出線段AB、AC、EF之間的數量關系。

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB⊥BC,DC⊥BC,AE 平分∠BAD,DE 平分∠ADC,以下結論:①∠AED=90°;②點 E 是 BC 的中點;③DE=BE;④AD=AB+CD;其中正確的是( )
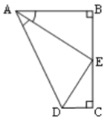
A. ①②③ B. ①②④ C. ①③④ D. ②③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線C:y=x2﹣2x+1的頂點為P,與y軸的交點為Q,點F(1, ![]() ).
).
(1)求tan∠OPQ的值;
(2)將拋物線C向上平移得到拋物線C′,點Q平移后的對應點為Q′,且FQ′=OQ′.
①求拋物線C′的解析式;
②若點P關于直線Q′F的對稱點為K,射線FK與拋物線C′相交于點A,求點A的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC內接于⊙O,AB是直徑,⊙O的切線PC交BA的延長線于點P,OF∥BC交AC于點E,交PC于點F,連接AF;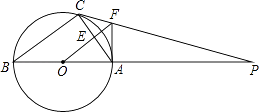
(1)判斷AF與⊙O的位置關系并說明理由.
(2)若⊙O的半徑為4,AF=3,求AC的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com