
如圖6,用水平線與豎直線將平面分成若干個邊長為1的正方形格子,點O、A、B均在正方形格子的頂點(格點)處,其中點O與點A位于同一水平線上,相距a格,點O與點B位于同一豎直線上,相距b格.
(1)若a=5,b=4,則△OAB中(包括三條邊)共有多少個格點?
(2)若a,b互質,則在線段AB上(不包括A、B兩點)是否有格點?證明你的結論.
(3)若a,b互質,且a>b>8,△OAB中(包括三條邊)共有67個格點,求a,b的值.
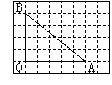
(1)如圖2,a=5,b=4,△OAB中(包括三條邊)的格點的個數為1+2+3+4+6=16.
(2)若a,b互質,假設線段AB上存在某一點P(恰為格點),可設點P到點O的水平距離為x,豎直距離為y(x,y均為整數),則
S△AOB= S△AOP+S△BOP=![]() ay+
ay+![]() bx,
bx,
所以![]() ab=
ab=![]() ay+
ay+![]() bx,
bx,
即ab=ay+bx,ay=b(a-x).
因為a,b互質,
所以a-x是a的倍數,它與a-x<a矛盾,
因此,假設不正確,即線段AB上(除A、B兩點外)不存在其它格點.
(3)由(2)知,線段AB上(除A、B兩點外)不存在其它的格點.
以OA、OB為邊作一個矩形OACB,則在△CAB中格點的個數與△OAB中格點的個數相同,且只有A、B兩點是公共的,而矩形OACB中格點的個數為(a+1)(b+1).
因此,(a+1)(b+1)+2=2×67=134,
(a+1)(b+1)=132=2×2×3×11.
由a>b>8,得a+1=12,b+1=11,
即a=11,b=10.


 新卷王期末沖刺100分系列答案
新卷王期末沖刺100分系列答案 全能闖關100分系列答案
全能闖關100分系列答案科目:初中數學 來源: 題型:

| 序號 | ① | ② | ③ | ④ | … |
| S | 2 | 2.5 | 3 | 4 | … |
| x | 4 | 5 | 6 | 8 | … |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中數學 來源: 題型:
| p |
| q |
| 1 |
| 3 |
 第
第查看答案和解析>>
科目:初中數學 來源: 題型:
| 1 |
| 2 |
| 1 |
| 2 |
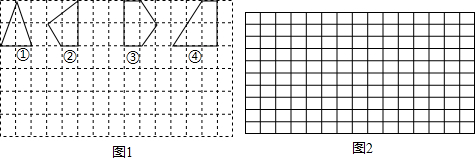
| 多邊形的序號 | ① | ② | ③ | ④ | … |
| 多邊形的面積S | 2 | 2.5 | 3 | 4 | … |
| 各邊上格點的個數和x | 4 | … |
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
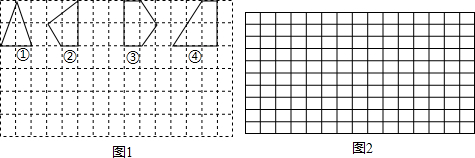
| 多邊形的序號 | ① | ② | ③ | ④ | … |
| 多邊形的面積S | 2 | 2.5 | 3 | 4 | … |
| 各邊上格點的個數和x | 4 | … |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com