解:(1)∵一個正數的平方根是3-a和2a+3,
∴3-a和2a+3互為相反數,
即(3-a)+(2a+3)=0;
解得a=-6,
則3-a=9;
則這個數為9
2=81;
故答案為:81,
(2)∵x
2+2x+y
2-6y+10=0,
∴(x+1)
2+(y-3)
2=0,
∴x+1=0,y-3=0,
∴x=-1,y=3,
則x
y=-1,
故答案為:-1,
(3)解:∵
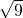
<

<
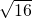
,
∴3<

<4,
∴2<6-

<3,
∴a=2,
∴b=6-

-2=4-

,
∴2a-b=2×2-(4-

)=

.
故答案是

.
(4)
1)將△ABP繞頂點A旋轉到△ACP′處,
∴△BAP≌△CAP′,
∴AB=AC,AP=AP′,∠BAP=∠CAP′,
∴∠BAC=PAP′=60°,
∴△APP′是等邊三角形,
∴∠APP′=60°,
因為B P P′不一定在一條直線上
連接PC,△PP′C是直角三角形,∠APB=∠AP′C=150°,
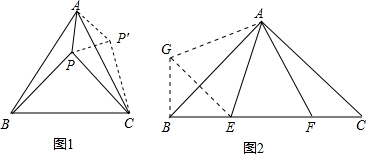
∴∠BPA=150°;
故答案是:②60,等邊,60,③直角,90°,150°;
2)把△ACF繞點A順時針旋轉90°,得到△ABG.連接EG.
則△ACF≌△ABG.
∴AG=AF,BG=CF,∠ABG=∠ACF=45°.
∵∠BAC=90°,∠GAF=90°.
∴∠GAE=∠EAF=45°,
又AG=AF,AE=AE.
∴△AEG≌△AFE.
∴EF=EG,
又∠GBE=90°,
∴BE
2+BG
2=EG
2,
即BE
2+CF
2=EF
2.
分析:(1)根據正數的平方根有兩個,且互為相反數,由此可得a的方程,解方程即可得到a的值;進而可得這個正數的平方根,最后可得這個正數的值.
(2)利用x
2+2x+y
2-6y+10=0,將原式配方得到(x+1)
2+(y-3)
2=0進而求出即可;
(3)先估算

的取值范圍,進而可求6-

的取值范圍,從而可求a,進而求b,最后把a、b的值代入計算即可.
(4)
1)此類題要充分運用旋轉的性質,以及全等三角形的性質得對應角相等,對應邊相等,得出∠PAP′=60°,再利用等邊三角形的判定得出△APP′為等邊三角形,即可得出∠APP′的度數,即可得出答案;
2)利用已知首先得出△AEG≌△AFE,即可把EF,BE,FC放到一個直角三角形中,從而根據勾股定理即可證明.
點評:此題主要考查了旋轉的性質、完全平方公式及非負數的性質、平方根的概念、無理數的估算等知識,充分運用全等三角形的性質找到相關的角和線段之間的關系以及確定無理數的整數部分是解決問題的關鍵.

 的整數部分和小數部分,則2a-b=______
的整數部分和小數部分,則2a-b=______
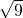 <
< <
<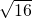 ,
, <4,
<4, <3,
<3, -2=4-
-2=4- ,
, )=
)= .
. .
.
 的取值范圍,進而可求6-
的取值范圍,進而可求6- 的取值范圍,從而可求a,進而求b,最后把a、b的值代入計算即可.
的取值范圍,從而可求a,進而求b,最后把a、b的值代入計算即可.
