



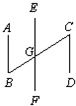
 ,
,


 學練快車道快樂假期暑假作業新疆人民出版社系列答案
學練快車道快樂假期暑假作業新疆人民出版社系列答案 浙大優學小學年級銜接導與練浙江大學出版社系列答案
浙大優學小學年級銜接導與練浙江大學出版社系列答案 小學暑假作業東南大學出版社系列答案
小學暑假作業東南大學出版社系列答案 津橋教育暑假拔高銜接廣東人民出版社系列答案
津橋教育暑假拔高銜接廣東人民出版社系列答案 波波熊暑假作業江西人民出版社系列答案
波波熊暑假作業江西人民出版社系列答案科目:初中數學 來源: 題型:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 12 |
| 5 |
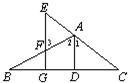
 cm,求CB的長.
cm,求CB的長.查看答案和解析>>
科目:初中數學 來源: 題型:
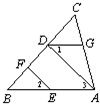
 說理填空:如圖直線a、b被直線c、d所截,且a∥b,∠1=70°,∠5=50°,這時∠2,∠3,∠4各是多少度?為什么?
說理填空:如圖直線a、b被直線c、d所截,且a∥b,∠1=70°,∠5=50°,這時∠2,∠3,∠4各是多少度?為什么?查看答案和解析>>
科目:初中數學 來源: 題型:閱讀理解
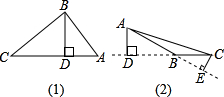
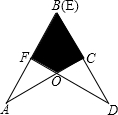 的交點.試說明不重疊的兩部分△AOF與△DOC全等的理由.
的交點.試說明不重疊的兩部分△AOF與△DOC全等的理由.查看答案和解析>>
科目:初中數學 來源: 題型:
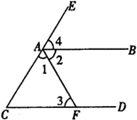 填空,完成下列說理過程
填空,完成下列說理過程查看答案和解析>>
科目:初中數學 來源: 題型:
 根據題意及解答過程填空:
根據題意及解答過程填空:| 1 |
| 3 |
| 1 |
| 3 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com