

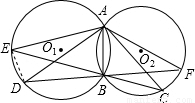
 證明:(1)∵AC為⊙O1的切線,
證明:(1)∵AC為⊙O1的切線,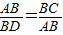 (3分)
(3分)

科目:初中數學 來源:2000年全國中考數學試題匯編《圓》(07)(解析版) 題型:解答題
查看答案和解析>>
科目:初中數學 來源:2000年全國中考數學試題匯編《圓》(01)(解析版) 題型:選擇題
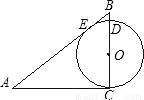



查看答案和解析>>
科目:初中數學 來源:2000年全國中考數學試題匯編《四邊形》(02)(解析版) 題型:填空題
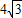 ,AD=
,AD=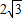 ,BD⊥AD,以BD為直徑的⊙O交AB于E,交CD于F,則?ABCD被⊙O所截得陰影部分的面積是 .
,BD⊥AD,以BD為直徑的⊙O交AB于E,交CD于F,則?ABCD被⊙O所截得陰影部分的面積是 .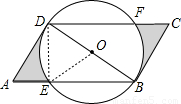
查看答案和解析>>
科目:初中數學 來源:2000年湖北省武漢市中考數學試卷(解析版) 題型:填空題
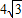 ,AD=
,AD=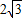 ,BD⊥AD,以BD為直徑的⊙O交AB于E,交CD于F,則?ABCD被⊙O所截得陰影部分的面積是 .
,BD⊥AD,以BD為直徑的⊙O交AB于E,交CD于F,則?ABCD被⊙O所截得陰影部分的面積是 .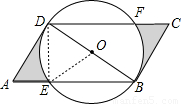
查看答案和解析>>
科目:初中數學 來源:2000年湖北省武漢市中考數學試卷(解析版) 題型:選擇題
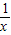 的圖象上的任意兩點,過A作x軸的垂線,垂足為B,過C作y軸的垂線,垂足為D,記Rt△AOB的面積為S1,Rt△COD的面積為S2,則( )
的圖象上的任意兩點,過A作x軸的垂線,垂足為B,過C作y軸的垂線,垂足為D,記Rt△AOB的面積為S1,Rt△COD的面積為S2,則( )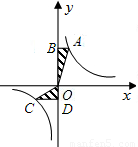
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com