
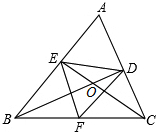
 如圖,在△ABC中,BD⊥AC于點(diǎn)D,CE⊥AB于點(diǎn)E,BD,CE交于點(diǎn)O,F(xiàn)為BC的中點(diǎn),連接EF,DF,DE,則下列結(jié)論:①EF=DF;②AD•AC=AE•AB;③△DOE∽△COB;④若∠ABC=45°時,BE=$\sqrt{2}$FC.
如圖,在△ABC中,BD⊥AC于點(diǎn)D,CE⊥AB于點(diǎn)E,BD,CE交于點(diǎn)O,F(xiàn)為BC的中點(diǎn),連接EF,DF,DE,則下列結(jié)論:①EF=DF;②AD•AC=AE•AB;③△DOE∽△COB;④若∠ABC=45°時,BE=$\sqrt{2}$FC.分析 ①由EF和DF均是斜邊BC邊上的中線可迅速作出判斷;
②由B、C、D、E四點(diǎn)共圓及割線定理迅速作出判斷;
③由B、C、D、E四點(diǎn)共圓可得出對應(yīng)圓周角相等,從而得出結(jié)論;
④若∠ABC=45°,則△BEC是等腰直角三角形,而F是BC中點(diǎn),從而結(jié)論顯然.
解答 解:∵BD⊥AC于點(diǎn)D,CE⊥AB于點(diǎn)E,F(xiàn)為BC的中點(diǎn),
∴EF=$\frac{1}{2}$BC,DF=$\frac{1}{2}$BC,
∴EF=DF,故①正確;
∵∠BEC=∠BDC=90°,
∴B、C、D、E四點(diǎn)共圓,
由割線定理可知AD•AC=AE•AB,故②正確;
∵B、C、D、E四點(diǎn)共圓,
∴∠OED=∠OBC,∠ODE=∠OCB,
∴△DOE∽△COB,故③正確;
若∠ABC=45°,則△BEC為等腰直角三角形,
∴BC=$\sqrt{2}$BE,
∵F為BC中點(diǎn),
∴FC=$\frac{1}{2}$BC=$\frac{\sqrt{2}}{2}$BE,
∴BE=$\sqrt{2}$FC,故④正確;
故答案為:①②③④.
點(diǎn)評 本題主要考查了直角三角形斜邊中線定理、四點(diǎn)共圓的判定與性質(zhì)、割線定理、相似三角形的判定與性質(zhì)、等腰直角三角形的判定與性質(zhì)等知識點(diǎn),難度不大,屬于常規(guī)題型.解答的關(guān)鍵是明確題目所給條件(比如中點(diǎn),垂直)與所學(xué)幾何定理的聯(lián)系.


 教材全解字詞句篇系列答案
教材全解字詞句篇系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:解答題
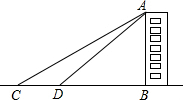 某班開展測量教學(xué)樓高度的綜合實(shí)踐活動.大家完成任務(wù)的方法有很多種,其中一種方法是:如圖,他們在C點(diǎn)測得教學(xué)樓AB的頂部點(diǎn)A的仰角為30°,然后向教學(xué)樓前進(jìn)20米到達(dá)點(diǎn)D,在點(diǎn)D測得點(diǎn)A的仰角為60°,且B,C,D三點(diǎn)在一條直線上.請你根據(jù)這些數(shù)據(jù),求出這幢教學(xué)樓AB的高度.
某班開展測量教學(xué)樓高度的綜合實(shí)踐活動.大家完成任務(wù)的方法有很多種,其中一種方法是:如圖,他們在C點(diǎn)測得教學(xué)樓AB的頂部點(diǎn)A的仰角為30°,然后向教學(xué)樓前進(jìn)20米到達(dá)點(diǎn)D,在點(diǎn)D測得點(diǎn)A的仰角為60°,且B,C,D三點(diǎn)在一條直線上.請你根據(jù)這些數(shù)據(jù),求出這幢教學(xué)樓AB的高度.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
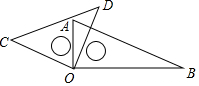 如圖,小明將自己用的一副三角板擺成如圖形狀,下列結(jié)論錯誤的是( )
如圖,小明將自己用的一副三角板擺成如圖形狀,下列結(jié)論錯誤的是( )| A. | ∠COA=∠DOB | B. | ∠AOD=∠B | C. | ∠COA與∠DOA互余 | D. | ∠AOD與∠COB互補(bǔ) |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
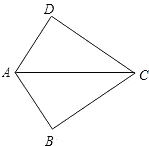 如圖,已知AB=AD,那么添加下列一個條件后,仍無法判定△ABC≌△ADC的是( )
如圖,已知AB=AD,那么添加下列一個條件后,仍無法判定△ABC≌△ADC的是( )| A. | CB=CD | B. | ∠BAC=∠DAC | ||
| C. | ∠BCA=∠DCA | D. | ∠B=∠D=90°,∠DAC=56°,∠BCA=34° |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 兩點(diǎn)確定一條直線 | B. | 兩點(diǎn)確定一條線段 | ||
| C. | 兩點(diǎn)之間線段最短 | D. | 兩點(diǎn)之間直線最短 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | $\frac{1}{2}$S=ah | B. | 2S=ah | C. | S-h=$\frac{1}{2}$a | D. | $\frac{S}{2a}$=h |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
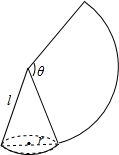 如圖,沿一條母線將圓錐側(cè)面剪開并展開,得到一個扇形,若圓錐的底面圓的半徑r=2cm,扇形的圓心角θ=120°,則該圓錐的母線長為( )
如圖,沿一條母線將圓錐側(cè)面剪開并展開,得到一個扇形,若圓錐的底面圓的半徑r=2cm,扇形的圓心角θ=120°,則該圓錐的母線長為( )| A. | 6cm | B. | 7cm | C. | 8cm | D. | 9cm |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com