
【題目】如圖所示,下列各組角的位置,判斷錯誤的是( ) 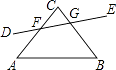
A.∠C和∠CFG是同旁內角
B.∠CGF和∠AFG是內錯角
C.∠BGF和∠A是同旁內角
D.∠BGF和∠AFD是同位角
【答案】C
【解析】解:A、在截線的同側,并且在被截線之間的兩個角是同旁內角,∠C和∠CFG符合同旁內角的定義,正確;
B、在截線的兩側,并且在被截線之間的兩個角是內錯角,∠CGF和∠AFG符合內錯角的定義,正確;
C、在截線的同側,并且在被截線的之間的兩個角是同旁內角,∠BGF和∠A不符合同旁內角的定義,錯誤;
D、在截線的同側,并且在被截線的同一方的兩個角是同位角,∠BGF和∠AFD符合同位角的定義,正確.
故選C.
【考點精析】本題主要考查了同位角、內錯角、同旁內角的相關知識點,需要掌握兩條直線被第三條直線所截形成八個角,它們構成了同位角、內錯角與同旁內角;判別同位角、內錯角或同旁內角的關鍵是找到構成這兩個角的“三線”,有時需要將有關的部分“抽出”或把無關的線略去不看,有時又需要把圖形補全才能正確解答此題.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖,已知△ABC為直角三角形,∠C=90°,邊BC是⊙O的切線,切點為D,AB經過圓心O并與圓相交于點E,連接AD.
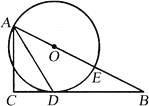
(1)求證:AD平分∠BAC;
(2)若AC=8,tan∠DAC=![]() ,求⊙O的半徑.
,求⊙O的半徑.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知∠ABC=90°,D是直線AB上的點,AD=BC.過點A作AF⊥AB,并截取AF=BD,連接DC,DF,CF. 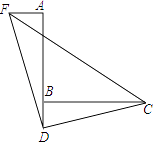
(1)判斷△CDF的形狀并證明.
(2)若BC=6,AF=2,求AB的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】求兩個正整數的最大公約數是常見的數學問題,中國古代數學專著《九章算術》中便記載了求兩個正整數最大公約數的一種方法﹣﹣更相減損術,術曰:“可半者半之,不可半者,副置分母、子之數,以少成多,更相減損,求其等也.以等數約之”,意思是說,要求兩個正整數的最大公約數,先用較大的數減去較小的數,得到差,然后用減數與差中的較大數減去較小數,以此類推,當減數與差相等時,此時的差(或減數)即為這兩個正整數的最大公約數.
例如:求91與56的最大公約數
解:
請用以上方法解決下列問題:
(1)求108與45的最大公約數;
(2)求三個數78、104、143的最大公約數.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某地區住宅用電之電費計算規則如下:每月每戶不超過50度時,每度以4元收費;超過50度的部分,每度以5元收費,并規定用電按整數度計算(小數部份無條件舍去) .
(1)下表給出了今年3月份A,B兩用戶的部分用電數據,請將表格數據補充完整,
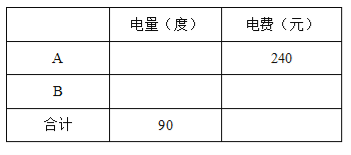
(2)若假定某月份C用戶比D用戶多繳電費38元,求C用戶該月可能繳的電費為多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com