
閱讀下面的材料:
小明在學(xué)習(xí)中遇到這樣一個(gè)問題:若1≤x≤m,求二次函數(shù)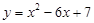 的最大值.他畫圖研究后發(fā)現(xiàn),
的最大值.他畫圖研究后發(fā)現(xiàn), 和
和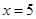 時(shí)的函數(shù)值相等,于是他認(rèn)為需要對(duì)
時(shí)的函數(shù)值相等,于是他認(rèn)為需要對(duì) 進(jìn)行分類討論.他的解答過程如下:
進(jìn)行分類討論.他的解答過程如下: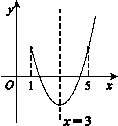
∵二次函數(shù)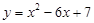 的對(duì)稱軸為直線
的對(duì)稱軸為直線 ,
,
∴由對(duì)稱性可知, 和
和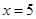 時(shí)的函數(shù)值相等.
時(shí)的函數(shù)值相等.
∴若1≤m<5,則 時(shí),
時(shí), 的最大值為2;
的最大值為2;
若m≥5,則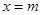 時(shí),
時(shí), 的最大值為
的最大值為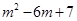 .
.
請(qǐng)你參考小明的思路,解答下列問題:
(1)當(dāng)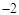 ≤x≤4時(shí),二次函數(shù)
≤x≤4時(shí),二次函數(shù)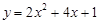 的最大值為_______;
的最大值為_______;
(2)若p≤x≤2,求二次函數(shù)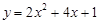 的最大值;
的最大值;
(3)若t≤x≤t+2時(shí),二次函數(shù)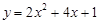 的最大值為31,則
的最大值為31,則 的值為_______.
的值為_______.
解:(1)∵拋物線的對(duì)稱軸為直線x=-1,
∴當(dāng)-2≤x≤4時(shí),二次函數(shù)y=2x2+4x+1的最大值為:2×42+4×4+1=49;
(2)∵二次函數(shù)y=2x2+4x+1的對(duì)稱軸為直線x=-1,
∴由對(duì)稱性可知,當(dāng)x=-4和x=2時(shí)函數(shù)值相等,
∴若p≤-4,則當(dāng)x=p時(shí),y的最大值為2p2+4p+1,
若-4<p≤2,則當(dāng)x=2時(shí),y的最大值為17;
(3)t<-2時(shí),最大值為:2t2+4t+1=31,
整理得,t2+2t-15=0,
解得t1=3(舍去),t2=-5,
t≥-2時(shí),最大值為:2(t+2)2+4(t+2)+1=31,
整理得,(t+2)2+2(t+2)-15=0,
解得t1=1,t2=-7(舍去),
所以,t的值為1或-5.
解析試題分析:(1)先求出拋物線的對(duì)稱軸為直線x=-1,然后確定當(dāng)x=4時(shí)取得最大值,代入函數(shù)解
析式進(jìn)行計(jì)算即可得解;(2)先求出拋物線的對(duì)稱軸為直線x=-1,再根據(jù)對(duì)稱性可得x=-4和x=2
時(shí)函數(shù)值相等,然后分p≤-4,-4<p≤2討論求解;(3)根據(jù)(2)的思路分t<-2,t≥-2時(shí)兩
種情況討論求解.
考點(diǎn):二次函數(shù)的最值
點(diǎn)評(píng):本題考查了二次函數(shù)的最值問題,主要利用了二次函數(shù)的對(duì)稱性,確定出拋物線的對(duì)稱軸解析式是確定p和t的取值范圍的關(guān)鍵,難點(diǎn)在于讀懂題目信息.


 輕巧奪冠周測(cè)月考直通中考系列答案
輕巧奪冠周測(cè)月考直通中考系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:單選題
如圖,△ABC與△A′B′C′關(guān)于直線 對(duì)稱,則∠B的度數(shù)為( )
對(duì)稱,則∠B的度數(shù)為( )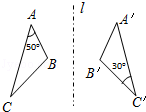
| A.30° | B.50° | C.90° | D.100° |
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com