名校通行證有效作業系列答案科目：初中數學 來源：2018年秋人教版八年級數學上冊 第11-13章 綜合測試卷 題型：單選題
如圖，在△ABC中，CD是AB邊上的高，BE是AC邊的高，點O是兩條高的交點，則∠A與∠1＋∠2的大小關系是( )
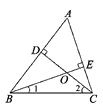
A. ∠A＞∠1＋∠2 B. ∠A=∠1＋∠2
C. ∠A＜∠1＋∠2 D. 無法確定
查看答案和解析>>
科目：初中數學 來源：廣西桂林市灌陽縣2019屆九年級上學期期中考試數學試卷 題型：單選題
如圖，函數y1=x﹣1和函數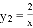
的圖象相交于點M（2，m），N（﹣1，n），若y1＞y2，則x的取值范圍是（ ）
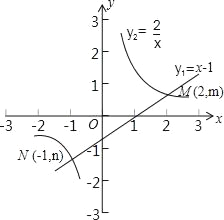
A. x＜﹣1或0＜x＜2 B. x＜﹣1或x＞2
C. ﹣1＜x＜0或0＜x＜2 D. ﹣1＜x＜0或x＞2
查看答案和解析>>
科目：初中數學 來源：人教版九年級數學下冊第二十六章反比例函數 單元檢測卷 題型：解答題
已知反比例函數的圖象經過點P（2，﹣3）．
（1）求該函數的解析式；
（2）若將點P沿x軸負方向平移3個單位，再沿y軸方向平移n（n＞0）個單位得到點P′，使點P′恰好在該函數的圖象上，求n的值和點P沿y軸平移的方向．
查看答案和解析>>
科目：初中數學 來源：山西省2018屆九年級中考模擬百校聯考（一）數學試卷 題型：解答題
綜合與實踐 美妙的黃金矩形
閱讀理解
在數學上稱短邊與長邊的比是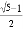
（約為0.618）的矩形叫做黃金矩形（GoldenRectangle），黃金矩形蘊藏著豐富的美學價值，給我們以協調、勻稱的美感．
（1）某校團委舉辦“五•四手抄報比賽”，手抄報規格統一設計成：長是40cm的黃金矩形，則寬約為__________cm；（精確到0.1cm）
操作發現 利用一張正方形紙片折疊出一個黃金矩形．
第一步，如圖1，折疊正方形紙片ABCD，使AB和DC重合，得到折痕EF（點E，F分別在邊AD，BC上），然后把紙片展平．
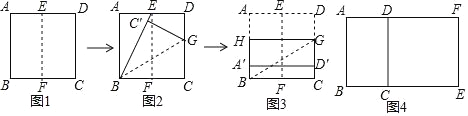
第二步，如圖2，折疊正方形紙片ABCD，使得BC落在BE上，點C′和點C對應，得到折痕BG（點G在CD上），再次紙片展平．
第三步，如圖3，沿過點G的直線折疊正方形紙片ABCD，使點A和點D分別落在AB和CD上，折痕為HG，顯然四邊形HBCG為矩形．
（2）在上述操作中，以AB=2為例，證明矩形HBCG是黃金矩形．
（參考計算：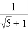
=
）
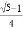拓廣探索
（3）“希望小組”的同學通過探究發現：以黃金矩形的長邊為一邊，在原黃金矩形外作正方形，得到的新矩形仍然是黃金矩形．
如圖4，如果四邊形ABCD是黃金矩形（AB＞AD），四邊形DCEF是正方形，那么四邊形ABEF也是黃金矩形，他們的發現正確嗎？請說明理由．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
________．
，則
的值是 
B．
C．
D．
，
，則
B. 
C. 
D. 