
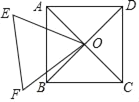
【題目】如圖,正方形ABCD的對角線相交于點O,正三角形OEF繞點O旋轉,在旋轉過程中,當CF=DE時,∠DOF的大小是_____.
【答案】165°或15°.
【解析】
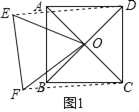
如圖1,連結CF、DE,根據正方形與等邊三角形的性質得OC=OD,∠COD=90°,OE=OF,∠EOF=60°,根據“SSS”可判斷△ODE≌△OCF,則∠DOE=∠COF,于是可求∠DOF;如圖2,同理可證得△ODE≌△OCF,所以∠DOE=∠COF,于是可求∠DOF.
解:如圖1,連結CF、DE,
∵四邊形ABCD為正方形,
∴OC=OD,∠COD=90°,
∵△OEF為等邊三角形,
∴OE=OF,∠EOF=60°,
在△ODE和△OCF中
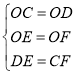 ,
,
∴△ODE≌△OCF(SSS),
∴∠DOE=∠COF=![]() ×(360°﹣90°﹣60°)=105°,
×(360°﹣90°﹣60°)=105°,
∴∠DOF=∠DOE+60°=165°;
如圖2,
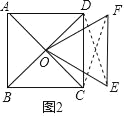
在△ODE和△OCF中,
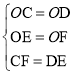 ,
,
∴△ODE≌△OCF(SSS),
∴∠DOE=∠COF,
∴∠DOF=∠COE,
∴∠DOF=![]() ×(90°﹣60°)=15°.
×(90°﹣60°)=15°.
∴∠DOF的大小是165°或15°.
故答案為:165°或15°.


科目:初中數學 來源: 題型:
【題目】小穎和小紅兩位同學在學習“概率”時,做擲骰子(質地均勻的正方體)試驗.
(1)她們在一次試驗中共擲骰子60次,試驗的結果如下:
朝上的點數 | 1 | 2 | 3 | 4 | 5 | 6 |
出現的次數 | 7 | 9 | 6 | 8 | 20 | 10 |
①填空:此次試驗中“5點朝上”的頻率為____;
②小紅說:“根據試驗,出現5點的概率最大.”她的說法正確嗎?為什么?
(2)小穎和小紅在試驗中如果各擲一枚骰子,那么兩枚骰子朝上的點數之和為多少時的概率最大?試用列表法或畫樹狀圖的方法加以說明,并求出其最大概率
查看答案和解析>>
科目:初中數學 來源: 題型:
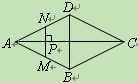
【題目】如圖,點P是菱形ABCD的對角線AC上的一個動點,過點P垂直于AC的直
線交菱形ABCD的邊于M、N兩點.設AC=2,BD=1,AP=x,△AMN的面積為y,則
y關于x的函數圖象大致形狀是【 】

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,A點坐標為(3,4),將線段OA繞原點O逆時針旋轉90°得到線段OA′,則點A′的坐標是( )
A. (﹣4,3) B. (﹣3,4)
C. (3,﹣4) D. (4,﹣3)
查看答案和解析>>
科目:初中數學 來源: 題型:
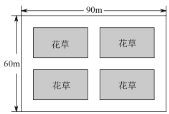
【題目】成都市中心城區“小游園,微綠地”規劃已經實施,武侯區某街道有一塊矩形空地進入規劃試點.如圖,已知該矩形空地長為![]() ,寬為
,寬為![]() ,按照規劃將預留總面積為
,按照規劃將預留總面積為![]() 的四個小矩形區域(陰影部分)種植花草,并在花草周圍修建三條橫向通道和三條縱向通道,各通道的寬度相等.
的四個小矩形區域(陰影部分)種植花草,并在花草周圍修建三條橫向通道和三條縱向通道,各通道的寬度相等.
(1)求各通道的寬度;
(2)現有一工程隊承接了對這![]() 的區域(陰影部分)進行種植花草的綠化任務,該工程隊先按照原計劃進行施工,在完成了
的區域(陰影部分)進行種植花草的綠化任務,該工程隊先按照原計劃進行施工,在完成了![]() 的綠化任務后,將工作效率提高
的綠化任務后,將工作效率提高![]() ,結果提前
,結果提前![]() 天完成任務,求該工程隊原計劃每天完成多少平方米的綠化任務?
天完成任務,求該工程隊原計劃每天完成多少平方米的綠化任務?
查看答案和解析>>
科目:初中數學 來源: 題型:
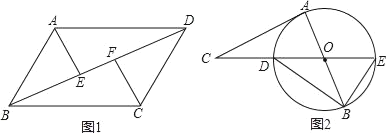
【題目】(1)已知,如圖①,在平行四邊形ABCD中,E、F是對角線BD上的兩點,且BF=DE.求證:AE=CF;
(2)已知,如圖②,AB是⊙O的直徑,CA與⊙O相切于點A.連接CO交⊙O于點D,CO的延長線交⊙O于點E.連接BE、BD,∠ABD=30°,求∠EBO和∠C的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】調查作業:了解你所住小區家庭3月份用氣量情況
小天、小東和小蕓三位同學住在同一小區,該小區共有300戶家庭,每戶家庭人數在2~5之間,這300戶家庭的平均人數約為3.3.
小天、小東、小蕓各自對該小區家庭3月份用氣量情況進行了抽樣裯查,將收集的數據進行了整理,繪制的統計表分別為表1、表2和表3.
表1抽樣調查小區4戶家庭3月份用氣量統計表(單位:m3)
家庭人數 | 2 | 3 | 4 | 5 |
用氣量 | 14 | 19 | 21 | 26 |
表2抽樣調查小區15戶家庭3月份用氣量統計表(單位:m3)
家庭人數 | 2 | 2 | 2 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 4 |
用氣量 | 10 | 11 | 15 | 13 | 14 | 15 | 15 | 17 | 17 | 18 | 18 | 18 | 20 | 22 |
表3抽樣調查小區15戶家庭3月份用氣量統計表(單位:m3)
家庭人數 | 2 | 2 | 2 | 3 | 3 | 3 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 5 | 5 |
用氣量 | 10 | 12 | 13 | 14 | 17 | 17 | 18 | 20 | 20 | 21 | 22 | 26 | 31 | 28 | 31 |
根據以|材料回答問題:
(1)小天、小東和小蕓三人中,哪位同學抽樣調查的數據能較好地反映出該小區家庭3月份用氣量情況?請簡要說明其他兩位同學抽樣調查的不足之處.
(2)在表3中,調查的15個家庭中使用氣量的中位數是 m3,眾數是 m3.
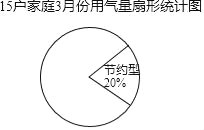
(3)小東將表2中的數據按用氣量x(m3)大小分為三類.
①節約型:10≤x≤13,②適中型:14≤x≤17,③偏高型:18≤x≤22,并繪制成如圖扇形統訃圖,請幫助他將扇形圖補充完整.
(4)小蕓算出表3中3月份平均每人的用氣量為6m3,請估計該小區3月份的總用氣量.
查看答案和解析>>
科目:初中數學 來源: 題型:
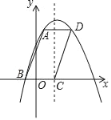
【題目】如圖,ABCD與拋物線y=﹣x2+bx+c相交于點A,B,D,點C在拋物線的對稱軸上,已知點B(﹣1,0),BC=4.
(1)求拋物線的解析式;
(2)求BD的函數表達式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線y=ax2+bx+3與x軸交于點A(﹣1,0),B(3,0).
(1)求拋物線的解析式;
(2)過點D(0,![]() )作x軸的平行線交拋物線于E,F兩點,求EF的長;
)作x軸的平行線交拋物線于E,F兩點,求EF的長;
(3)當y≤![]() 時,直接寫出x的取值范圍是 .
時,直接寫出x的取值范圍是 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com