
【題目】如圖,![]() O的直徑AB長為12,點E是半徑OA的中點,過點E作CD⊥AB交
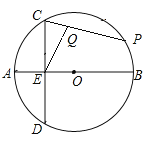
O的直徑AB長為12,點E是半徑OA的中點,過點E作CD⊥AB交![]() O于點C、D,點P在
O于點C、D,點P在![]() 上運動,點Q在線段CP上,且PQ=2CQ,則EQ的最大值是_________.
上運動,點Q在線段CP上,且PQ=2CQ,則EQ的最大值是_________.
【答案】![]()
【解析】
延長CD到M點,使DM=DE,連接MP,可根據三角形相似求得EQ的長度等于![]() MP,當MP經過圓心時,此時MP有最大值,EQ為最大值,連接OD,根據勾股定理求出DE、OM,即可求得MP的長,則可求得EQ的最大值.
MP,當MP經過圓心時,此時MP有最大值,EQ為最大值,連接OD,根據勾股定理求出DE、OM,即可求得MP的長,則可求得EQ的最大值.
連接OD,延長CD到M點,使DM=DE,連接MO并延長交圓O與P點,此時MP有最大值.
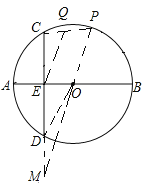
延長CD到M點,使DM=DE,連接MP,
∵CD⊥AB
∴CE=DE=DM
∵PQ=2CQ,EM=2CE
∴![]()
又∠C=∠C
∴△QCE∽△PCM
∴![]()
∴EQ=![]() MP
MP
當MP經過圓心時,此時MP有最大值,則EQ為最大值,
連接OD,
∵![]() O的直徑AB長為12,點E是半徑OA的中點,CD⊥AB
O的直徑AB長為12,點E是半徑OA的中點,CD⊥AB
∴OD=6,OE=3,
∴DE=![]()
∴EM=6![]()
∴OM=![]()
∴MP=OM+OP=![]()
∴EQ=![]() MP
MP![]()
故答案為:![]()


科目:初中數學 來源: 題型:
【題目】如圖,在正方形![]() 中,
中,![]() ,點
,點![]() 在正方形邊上沿
在正方形邊上沿![]() 運動(含端點),連接
運動(含端點),連接![]() ,以
,以![]() 為邊,在線段右側作正方形
為邊,在線段右側作正方形![]() ,連接
,連接![]() 、
、![]() .
.
小穎根據學習函數的經驗,在點![]() 運動過程中,對線段
運動過程中,對線段![]() 、
、![]() 、
、![]() 的長度之間的關系進行了探究.
的長度之間的關系進行了探究.
下面是小穎的探究過程,請補充完整:
(1)對于點![]() 在
在![]() 、
、![]() 邊上的不同位置,畫圖、測量,得到了線段
邊上的不同位置,畫圖、測量,得到了線段![]() 、
、![]() 、
、![]() 的長度的幾組值,如下表:
的長度的幾組值,如下表:
位置 | 位置 | 位置 | 位置 | 位置 | 位置 | 位置 | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
在![]() 、
、![]() 和
和![]() 的長度這三個量中,確定 的長度是自變量, 的長度和 的長度都是這個自變量的函數.
的長度這三個量中,確定 的長度是自變量, 的長度和 的長度都是這個自變量的函數.
(2)在同一平面直角坐標系![]() 中,畫出(1)中所確定的函數的圖象:
中,畫出(1)中所確定的函數的圖象:
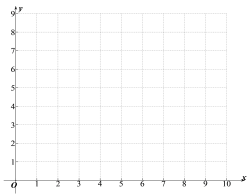
(3)結合函數圖像,解決問題:
當![]() 為等腰三角形時,
為等腰三角形時,![]() 的長約為
的長約為
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】《九章算術》是我國古代數學的經典著作,書中有一個問題:“今有黃金九枚,白銀一十一枚,稱之重適等.交易其一,金輕十三兩.問金、銀一枚各重幾何?”.意思是:今有甲種袋子中裝有黃金9枚(每枚黃金重量相同),乙種袋子中裝有白銀11枚(每枚白銀重量相同),稱重兩袋相等.兩袋互相交換1枚后,甲種袋子比乙種袋子輕了13兩(袋子重量忽略不計).問黃金、白銀每枚各重多少兩?設每枚黃金重x兩,每枚白銀重y兩,則可建立方程為( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線![]() 與雙曲線
與雙曲線![]() 在第一象限內交于
在第一象限內交于![]() 、
、![]() 兩點,已知
兩點,已知![]() ,
,![]() .
.

(1)![]() __________,
__________,![]() ____________________,
____________________,![]() ____________________.
____________________.
(2)直接寫出不等式![]() 的解集;
的解集;
(3)設點![]() 是線段
是線段![]() 上的一個動點,過點
上的一個動點,過點![]() 作
作![]() 軸于點
軸于點![]() ,
,![]() 是
是![]() 軸上一點,求
軸上一點,求![]() 的面積
的面積![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,為了測量山腳到塔頂的高度(即![]() 的長),某同學在山腳
的長),某同學在山腳![]() 處用測角儀測得塔頂
處用測角儀測得塔頂![]() 的仰角為
的仰角為![]() ,再沿坡度為
,再沿坡度為![]() 的小山坡前進400米到達點
的小山坡前進400米到達點![]() ,在
,在![]() 處測得塔頂
處測得塔頂![]() 的仰角為
的仰角為![]() .
.
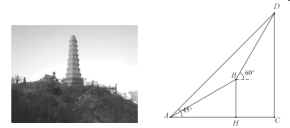
(1)求坡面![]() 的鉛垂高度(即
的鉛垂高度(即![]() 的長);
的長);
(2)求![]() 的長.(結果保留根號,測角儀的高度忽略不計).
的長.(結果保留根號,測角儀的高度忽略不計).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】定義:三角形一邊上的點將該邊分為兩條線段,且這兩條線段的積等于這個點到該邊所對頂點連線的平方,則稱這個點為三角形該邊的“好點”.如圖1,△ABC中,點D是BC邊上一點,連結AD,若![]() ,則稱點D是△ABC中BC邊上的“好點”.
,則稱點D是△ABC中BC邊上的“好點”.
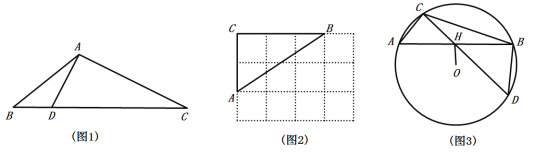
(1)如圖2,△ABC的頂點是![]() 網格圖的格點,請僅用直尺畫出AB邊上的一個“好點”.
網格圖的格點,請僅用直尺畫出AB邊上的一個“好點”.
(2)△ABC中,BC=9,![]() ,
,![]() ,點D是BC邊上的“好點”,求線段BD的長.
,點D是BC邊上的“好點”,求線段BD的長.
(3)如圖3,△ABC是![]() 的內接三角形,OH⊥AB于點H,連結CH并延長交
的內接三角形,OH⊥AB于點H,連結CH并延長交![]() 于點D.
于點D.
①求證:點H是△BCD中CD邊上的“好點”.
②若![]() 的半徑為9,∠ABD=90°,OH=6,請直接寫出
的半徑為9,∠ABD=90°,OH=6,請直接寫出![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
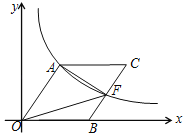
【題目】如圖,O為坐標原點,點B在x軸的正半軸上,四邊形OACB是平行四邊形,點A的橫縱坐標之比為3:4,反比例函數y=![]() (k>0)在第一象限內的圖象經過點A,且與BC交于點F.
(k>0)在第一象限內的圖象經過點A,且與BC交于點F.
(1)若OA=10,求反比例函數解析式;
(2)若點F為BC的中點,且△AOF的面積S=12,求OA的長和點C的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
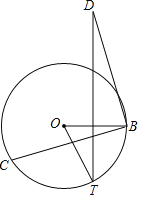
【題目】如圖,C為圓O上一動點(不與點B重合),點T為圓O上一動點,且∠BOT=60°,將BC繞點B順時針旋轉90°得到BD,連接TD,當TD最大時,∠BDT的度數為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】現有三張分別標有數字![]() 、
、![]() 、
、![]() 的卡片,它們除了數字外完全相同,把卡片背面朝上洗勻,從中任意抽取一張,將上面的數字記為
的卡片,它們除了數字外完全相同,把卡片背面朝上洗勻,從中任意抽取一張,將上面的數字記為![]() (不放回),再從中任意抽取一張,將上面的數字記為
(不放回),再從中任意抽取一張,將上面的數字記為![]() ,這樣的數字
,這樣的數字![]() ,
,![]() 能使關于
能使關于![]() 的一元二次方程
的一元二次方程![]() 有兩個正根的概率為________.
有兩個正根的概率為________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com