
【題目】如圖,平行四邊形![]() 分別切
分別切![]() 于點
于點![]() ,連接
,連接![]() 并延長交
并延長交![]() 于點
于點![]() ,連接
,連接![]() 與
與![]() 剛好平行,若
剛好平行,若![]() ,則
,則![]() 的直徑為______.
的直徑為______.
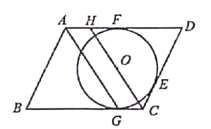
【答案】![]()
【解析】
先證得四邊形AGCH是平行四邊形,則![]() ,再證得
,再證得![]() ,求得
,求得![]()
![]() ,證得DO⊥HC,根據
,證得DO⊥HC,根據![]() ,即可求得半徑,從而求得結論.
,即可求得半徑,從而求得結論.
∵四邊形ABCD是平行四邊形,
∴AD∥BC,
∵AG∥HC,
∴四邊形AGCH是平行四邊形,
∴![]() ,
,
∵![]() 是⊙O的切線,且切點為
是⊙O的切線,且切點為![]() 、
、![]() ,
,
∴![]() ,∠GCH=∠HCD,
,∠GCH=∠HCD,
∵AD∥BC,
∴∠DHC=∠GCH,
∴∠DHC=∠HCD,
∴三角形DHC為等腰三角形,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
連接OD、OE,如圖,
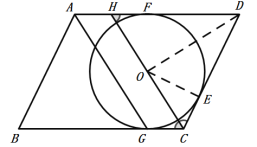
∵![]() 是⊙O的切線,且切點為
是⊙O的切線,且切點為![]() 、
、![]() ,
,
∴DO是∠FDE的平分線,
又∵![]() ,
,
∴DO⊥HC,
∴∠DOC=90![]() ,
,
∵![]() 切⊙O于
切⊙O于![]() ,
,
∴OE⊥CD,
∵∠OCE+∠COE=90![]() ,∠DOE+∠COE=90
,∠DOE+∠COE=90![]() ,
,
∴∠OCE=∠DOE,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∴⊙O的直徑為:![]()
故答案為:![]() .
.


 快樂5加2金卷系列答案
快樂5加2金卷系列答案科目:初中數學 來源: 題型:
【題目】縉云山是國家級自然風景名勝區,上周周末,小明和媽媽到縉云山游玩,登上了香爐峰觀景塔,從觀景塔底中心![]() 處水平向前走
處水平向前走![]() 米到
米到![]() 點處,再沿著坡度為
點處,再沿著坡度為![]() 的斜坡
的斜坡![]() 走一段距離到達
走一段距離到達![]() 點,此時回望觀景塔,更顯氣勢宏偉,在
點,此時回望觀景塔,更顯氣勢宏偉,在![]() 點觀察到觀景塔頂端的仰角為
點觀察到觀景塔頂端的仰角為![]() 再往前沿水平方向走
再往前沿水平方向走![]() 米到
米到![]() 處,觀察到觀景塔頂端的仰角是
處,觀察到觀景塔頂端的仰角是![]() ,則觀景塔的高度
,則觀景塔的高度![]() 為( )(tan22°≈0.4)
為( )(tan22°≈0.4)
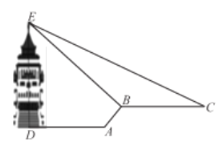
A.![]() 米B.
米B.![]() 米C.
米C.![]() 米D.
米D.![]() 米
米
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函數y=![]() 在第一象限的圖象經過點B,則OA2﹣AB2=_____.
在第一象限的圖象經過點B,則OA2﹣AB2=_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(2011山東濟南,27,9分)如圖,矩形OABC中,點O為原點,點A的坐標為(0,8),點C的坐標為(6,0).拋物線![]() 經過A、C兩點,與AB邊交于點D.
經過A、C兩點,與AB邊交于點D.
(1)求拋物線的函數表達式;
(2)點P為線段BC上一個動點(不與點C重合),點Q為線段AC上一個動點,AQ=CP,連接PQ,設CP=m,△CPQ的面積為S.
①求S關于m的函數表達式,并求出m為何值時,S取得最大值;
②當S最大時,在拋物線![]() 的對稱軸l上若存在點F,使△FDQ為直角三角形,請直接寫出所有符合條件的F的坐標;若不存在,請說明理由.
的對稱軸l上若存在點F,使△FDQ為直角三角形,請直接寫出所有符合條件的F的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了了解全校![]() 名同學對學校設置的體操、籃球、足球、跑步、舞蹈等課外活動項目的喜愛情況,在全校范圍內隨機抽取了若干名同學,對他們喜愛的項目(每人選一項)進行了問卷調查,將數據進行了統計,并繪制成了如圖所示的條形統計圖和扇形統計圖(均不完整),請回答下列問題.
名同學對學校設置的體操、籃球、足球、跑步、舞蹈等課外活動項目的喜愛情況,在全校范圍內隨機抽取了若干名同學,對他們喜愛的項目(每人選一項)進行了問卷調查,將數據進行了統計,并繪制成了如圖所示的條形統計圖和扇形統計圖(均不完整),請回答下列問題.
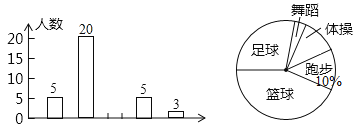
(1)在這次問卷調查中,共抽查了_________名同學;
(2)補全條形統計圖;
(3)估計該校![]() 名同學中喜愛足球活動的人數;
名同學中喜愛足球活動的人數;
(4)在體操社團活動中,由于甲、乙、丙、丁四人平時的表現優秀,現決定從這四人中任選兩名參加體操大賽.用樹狀圖或列表法求恰好選中甲、乙兩位同學的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,![]() 是
是![]() 的直徑,點
的直徑,點![]() 在
在![]() 上,
上,![]() ,FD切
,FD切![]() 于點
于點![]() ,連接
,連接![]() 并延長交
并延長交![]() 于點
于點![]() ,點
,點![]() 為
為![]() 中點,連接
中點,連接![]() 并延長交
并延長交![]() 于點
于點![]() ,連接
,連接![]() ,交
,交![]() 于點
于點![]() ,連接
,連接![]() .
.
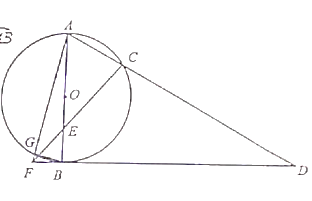
(1)求證:![]() ;
;
(2)若![]() 的半徑為
的半徑為![]() ,求
,求![]() 的長.
的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,直線
中,直線![]() 交
交![]() 軸于點
軸于點![]() ,交
,交![]() 軸于點
軸于點![]() ,
,![]() ,點
,點![]() 的坐標是
的坐標是![]() .
.
(1)如圖1,求直線![]() 的解析式;
的解析式;
(2)如圖2,點![]() 在第一象限內,連接
在第一象限內,連接![]() ,過點
,過點![]() 作
作![]() 交
交![]() 延長線于點
延長線于點![]() ,且
,且![]() ,過點
,過點![]() 作
作![]() 軸于點
軸于點![]() ,連接
,連接![]() ,設點
,設點![]() 的橫坐標為
的橫坐標為![]() ,
,![]() 的而積為S,求S與
的而積為S,求S與![]() 的函數關系式(不要求寫出自變量
的函數關系式(不要求寫出自變量![]() 的取值范圍);
的取值范圍);
(3)如圖3,在(2)的條件下,過點![]() 作
作![]() 軸,連接
軸,連接![]() 、
、![]() ,若
,若![]() ,
,![]() 時,求
時,求![]() 的值.
的值.
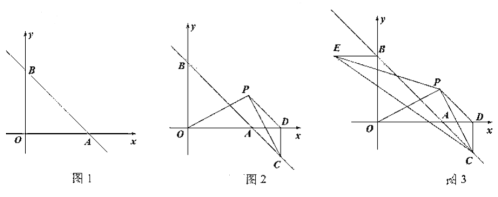
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為推進“傳統文化進校園”活動,某校準備成立“經典誦讀”、“傳統禮儀”、“民族器樂”和“地方戲曲”等四個課外活動小組.學生報名情況如圖(每人只能選擇一個小組):
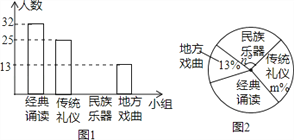
(1)報名參加課外活動小組的學生共有 人,將條形圖補充完整;
(2)扇形圖中m= ,n= ;
(3)根據報名情況,學校決定從報名“經典誦讀”小組的甲、乙、丙、丁四人中隨機安排兩人到“地方戲曲”小組,甲、乙恰好都被安排到“地方戲曲”小組的概率是多少?請用列表或畫樹狀圖的方法說明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】收發微信紅包已成為各類人群進行交流聯系,增強感情的一部分,下面是甜甜和她的雙胞胎妹妹在六一兒童節期間的對話.
請問:(1)2015年到2017年甜甜和她妹妹在六一收到紅包的年增長率是多少?
(2)2017年六一甜甜和她妹妹各收到了多少錢的微信紅包?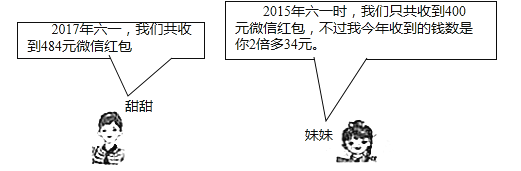
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com