
【題目】探索與研究:
方法1:如圖(a),對任意的符合條件的直角三角形繞其銳角頂點旋轉90°所得,所以
∠BAE=90°,且四邊形ACFD是一個正方形,它的面積和四邊形ABFE面積相等,而四邊形ABFE面積等于Rt△BAE和Rt△BFE的面積之和,根據圖示寫出證明勾股定理的過程;
方法2:如圖(b),是任意的符合條件的兩個全等的Rt△BEA和Rt△ACD拼成的,你能根據圖示再寫一種證明勾股定理的方法嗎?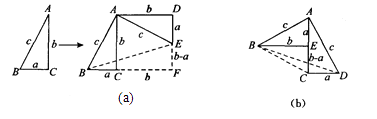
【答案】解:方法1:∵由圖(a)可知S正方形ACFD=S四邊形ABFE ,
∴S正方形ACFD=S⊿BAE+S⊿BFE
又∵正方形ACFD的邊長為b, SRt△BAE= ![]() ,SRt△BFE=
,SRt△BFE= ![]()
∴b2 = ![]() +
+ ![]()
即2b2 =c2 +(b+a)(b-a)
整理得: a2 +b2=c2
方法2:如圖(b)中,Rt△BEA和Rt△ACD全等, 設CD=a,AC=b,AD=c(b>a),
則AE=a,BE=b,AB=c,EC=b-a
由圖(b),S四邊形ABCD = SRt△BAE + SRt△ACD+SRt△BEC =SRt△BAD+S△BCD
又∵ SRt△BAE = ![]() , SRt△ACD =
, SRt△ACD = ![]() ,SRt△BEC =
,SRt△BEC = ![]() ,
,
SRt△BAD= ![]() ,S△BCD=
,S△BCD= ![]() ,
,
∴ ![]() +
+ ![]() +
+ ![]() =
= ![]() +
+ ![]()
即2ab+b(b-a) = c2 +a(b-a)
整理得: a2 +b2=c2
【解析】方法1:由S正方形ACFD=S⊿BAE+S⊿BFE,從而列出方程進行解答即可;
(2)方法2:由S四邊形ABCD = SRt△BAE + SRt△ACD+SRt△BEC =SRt△BAD+S△BCD,列方程解答即可。


 全能測控一本好卷系列答案
全能測控一本好卷系列答案 發散思維新課堂系列答案
發散思維新課堂系列答案科目:初中數學 來源: 題型:
【題目】模型建立:如圖1,等腰直角三角形ABC中,∠ACB=90°,CB=CA,直線ED經過點C,過A作AD⊥ED于D,過B作BE⊥ED于E.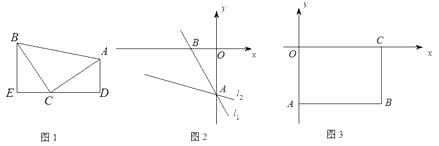
(1)求證:△BEC≌△CDA;
(2)模型應用:
①已知直線l1:y=- ![]() x-4與y軸交于A點,將直線l1繞著A點逆時針旋轉45°至l2 , 如圖2,求l2的函數解析式;
x-4與y軸交于A點,將直線l1繞著A點逆時針旋轉45°至l2 , 如圖2,求l2的函數解析式;
②如圖3,矩形ABCO,O為坐標原點,B的坐標為(8,-6),A、C分別在坐標軸上,P是線段BC上動點,設PC=m,已知點D在第四象限,且是直線y=-2x+6上的一點,若△APD是不以點A為直角頂點的等腰Rt△,請求出點D的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=BC,BE⊥AC于點E,AD⊥BC于點D,∠BAD=45°,AD與BE交于點F,連接CF.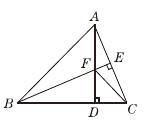
(1)求證:BF=2AE;
(2)若CD= ![]() ,求AD的長.
,求AD的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com