
 ;
;

 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:單選題
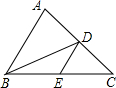 如圖,D,E分別是△ABC的邊AC,BC的中點,則下列說法錯誤的是
如圖,D,E分別是△ABC的邊AC,BC的中點,則下列說法錯誤的是查看答案和解析>>
科目:初中數學 來源: 題型:單選題
 如圖是某報記者在抽樣調查了一些市民八小時以外用于讀書的時間(單位:分鐘)后,繪制的頻率分布直方圖,圖中從左向右的前六個長方形的面積之和為0.95,200~230分鐘這一組的頻數是10,此次抽樣的樣本容量是
如圖是某報記者在抽樣調查了一些市民八小時以外用于讀書的時間(單位:分鐘)后,繪制的頻率分布直方圖,圖中從左向右的前六個長方形的面積之和為0.95,200~230分鐘這一組的頻數是10,此次抽樣的樣本容量是查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 書名 | 原價(元) |
| 中國歷史故事 | 50 |
| 名人名言 | 20 |
| 文化苦旅 | 28 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com