
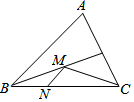
 如圖,在銳角三角形ABC中,BC=2,∠ABC=45°,BD平分∠ABC,M、N分別是BD、BC上的動點,則CM+MN的最小值為$\sqrt{2}$.
如圖,在銳角三角形ABC中,BC=2,∠ABC=45°,BD平分∠ABC,M、N分別是BD、BC上的動點,則CM+MN的最小值為$\sqrt{2}$. 分析 過點C作CE⊥AB于點E,交BD于點M′,過點M′作M′N′⊥BC,則CE即為CM+MN的最小值,再根據BC=4,∠ABC=45°,由銳角三角函數的定義即可求出CE的長.
解答  解:過點C作CE⊥AB于點E,交BD于點M′,過點M′作M′N′⊥BC,
解:過點C作CE⊥AB于點E,交BD于點M′,過點M′作M′N′⊥BC,
∵BD平分∠ABC,
∴M′E=M′N′,
∴M′N′+CM′=EM′+CM′=CE,則CE即為CM+MN的最小值,
∵BC=2,∠ABC=45°,
∴CE=BC•sin45°=2×$\frac{\sqrt{2}}{2}$=$\sqrt{2}$.
∴CM+MN的最小值是$\sqrt{2}$.
故答案是:$\sqrt{2}$.
點評 本題考查的是軸對稱-最短路線問題,根據題意作出輔助線,構造出直角三角形,利用銳角三角函數的定義求解是解答此題的關鍵.


 寒假學與練系列答案
寒假學與練系列答案科目:初中數學 來源: 題型:選擇題
| A. | 在一個僅裝著白球和黑球的袋中摸球,摸出紅球 | |
| B. | 在一個標準大氣壓下,加熱到100℃,水沸騰 | |
| C. | 有一名運動員奔跑的速度是30米/秒 | |
| D. | 購買一張福利彩票,中獎 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
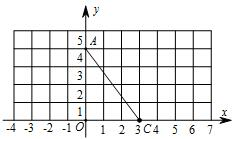 如圖,在平面直角坐標系中,A(0,4),C(3,0),
如圖,在平面直角坐標系中,A(0,4),C(3,0),查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com