Question

如圖，在等邊三角形ABC中，P為BC上一點，D為AC上一點，∠APD＝60°，BP＝1，CD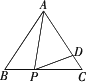＝，求△ABC的邊長．

Answer 1

答案：
解析：

分析：由圖形可以看出△APB與△PDC相似，只要能夠證明這一點，就可以由相似三角形的性質(zhì)建立對應邊之間的比例式，從而求出△ABC的邊長 　　解：設(shè)△ABC的邊長為x，則PC＝x－1． 　　在△APB和△PDC中，因為∠APB＝∠C＋∠PAC＝60°＋∠PAC，∠PDC＝∠APD＋∠PAC＝60°＋∠PAC，所以∠APB＝∠PDC． 　　又因為∠B＝∠C，所以△APB∽△PDC． 　　所以＝，即＝．解得x＝3． 　　經(jīng)檢驗，x＝3是原分式方程的解． 　　故△ABC的邊長為3． 　　點評：解決本題的關(guān)鍵是找到相似三角形，通過分析角之間的關(guān)系證明相似，然后運用性質(zhì)建立方程求解．