
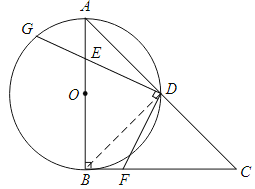
【題目】如圖,在RtΔABC中,∠ABC=90°,AB=CB,以AB為直徑的⊙O交AC于點D,點E是AB邊上一點(點E不與點A、B重合),DE的延長線交⊙O于點G,DF⊥DG,且交BC于點F.
(1)求證:AE=BF;
(2)連接EF,求證:∠FEB=∠GDA;
(3)連接GF,若AE=2,EB=4,求ΔGFD的面積.
【答案】(1)(2)見解析;(3)9
【解析】分析:(1)連接BD,由三角形ABC為等腰直角三角形,求出∠A與∠C的度數,根據AB為圓的直徑,利用圓周角定理得到∠ADB為直角,即BD垂直于AC,利用直角三角形斜邊上的中線等于斜邊的一半,得到AD=DC=BD=![]() AC,進而確定出∠A=∠FBD,再利用同角的余角相等得到一對角相等,利用ASA得到三角形AED與三角形BFD全等,利用全等三角形對應邊相等即可得證;
AC,進而確定出∠A=∠FBD,再利用同角的余角相等得到一對角相等,利用ASA得到三角形AED與三角形BFD全等,利用全等三角形對應邊相等即可得證;
(2)連接EF,BG,由三角形AED與三角形BFD全等,得到ED=FD,進而得到三角形DEF為等腰直角三角形,利用圓周角定理及等腰直角三角形性質得到一對同位角相等,利用同位角相等兩直線平行,再根據平行線的性質和同弧所對的圓周角相等,即可得出結論;
(3)由全等三角形對應邊相等得到AE=BF=1,在直角三角形BEF中,利用勾股定理求出EF的長,利用銳角三角形函數定義求出DE的長,利用兩對角相等的三角形相似得到三角形AED與三角形GEB相似,由相似得比例,求出GE的長,由GE+ED求出GD的長,根據三角形的面積公式計算即可.
詳解:(1)連接BD.在Rt△ABC中,∠ABC=90°,AB=BC,∴∠A=∠C=45°.
∵AB為圓O的直徑,∴∠ADB=90°,即BD⊥AC,∴AD=DC=BD=![]() AC,∠CBD=∠C=45°,∴∠A=∠FBD.
AC,∠CBD=∠C=45°,∴∠A=∠FBD.
∵DF⊥DG,∴∠FDG=90°,∴∠FDB+∠BDG=90°.
∵∠EDA+∠BDG=90°,∴∠EDA=∠FDB.在△AED和△BFD中,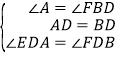 ,∴△AED≌△BFD(ASA),∴AE=BF;
,∴△AED≌△BFD(ASA),∴AE=BF;
(2)連接EF,BG.
∵△AED≌△BFD,∴DE=DF.
∵∠EDF=90°,∴△EDF是等腰直角三角形,∴∠DEF=45°.
∵∠G=∠A=45°,∴∠G=∠DEF,∴GB∥EF,∴∠FEB=∠GBA.
∵∠GBA=∠GDA,∴∠FEB=∠GDA;
(3)∵AE=BF,AE=2,∴BF=2.在Rt△EBF中,∠EBF=90°,∴根據勾股定理得:EF2=EB2+BF2.
∵EB=4,BF=2,∴EF=![]() =
=![]() .
.
∵△DEF為等腰直角三角形,∠EDF=90°,∴cos∠DEF=![]() .
.
∵EF=![]() ,∴DE=
,∴DE=![]() ×
×![]() =
=![]() .
.
∵∠G=∠A,∠GEB=∠AED,∴△GEB∽△AED,∴![]() =
=![]() ,即GEED=AEEB,∴
,即GEED=AEEB,∴![]() GE=8,即GE=
GE=8,即GE=![]() ,則GD=GE+ED=
,則GD=GE+ED=![]() .
.
∴![]() .
.



 課堂全解字詞句段篇章系列答案
課堂全解字詞句段篇章系列答案 步步高口算題卡系列答案
步步高口算題卡系列答案科目:初中數學 來源: 題型:
【題目】為了解我市家庭月均用電量情況,有關部門隨機抽查了我市1000戶家庭的月均用電量,并將調查數據整理如下:
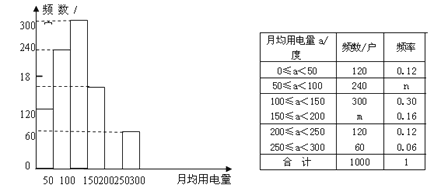
(1)頻數分布表中的m= ,n= ;
(2)補全頻數分布直方圖;
(3)被調查的1000戶家庭月均用電量的眾數落在哪一個范圍?
(4)求月均用電量小于150度的家庭數占被調查家庭總數的百分比.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校為提高學生體考成績,對全校300名九年級學生進行一分種跳繩訓練.為了解學生訓練效果,學校體育組在九年級上學期開學初和學期末分別對九年級學生進行一分種跳繩測試,學生成績均為整數,滿分20分,大于18分為優秀.現隨機抽取了同一部分學生的兩次成績進行整理、描述和分析.(成績得分用x表示,共分成五組:A.x<13,B.13≤x<15,C.15≤x<17,D.17≤x<19,E.19≤x≤20)
開學初抽取學生的成績在D組中的數據是:17,17,17,17,17,18,18.
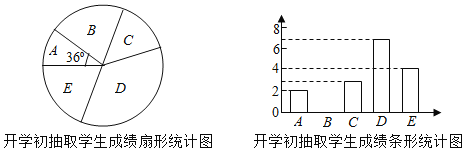
學期末抽取學生成績統計表
學生成績 | A組 | B組 | C組 | D組 | E組 |
人數 | 0 | 1 | 4 | 5 | a |
分析數據:
平均數 | 中位數 | 眾數 | |
開學初抽取學生成績 | 16 | b | 17 |
學期末抽取學生成績 | 18 | 18.5 | 19 |
根據以上信息,解答下列問題:
(1)直接寫出圖表中a、b的值,并補全條形統計圖;
(2)假設該校九年級學生都參加了兩次測試,估計該校學期末成績優秀的學生人數比開學初成績優秀的學生人數增加了多少?
(3)小莉開學初測試成績16分,學期末測試成績19分,根據抽查的相關數據,請選擇一個合適的統計量評價小莉的訓練效果.
查看答案和解析>>
科目:初中數學 來源: 題型:
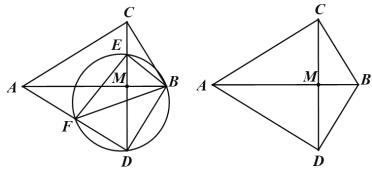
【題目】如圖,在△ABC中,∠ACB=90°,將△ABC沿直線AB翻折得到△ABD,連接CD交AB于點M.E是線段CM上的點,連接BE.F是△BDE的外接圓與AD的另一個交點,連接EF,BF,
(1)求證:△BEF是直角三角形;
(2)求證:△BEF∽△BCA;
(3)當AB=6,BC=m時,在線段CM正存在點E,使得EF和AB互相平分,求m的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知D、E、F分別是等邊△ABC的邊AB、BC、AC上的點,且DE⊥BC、EF⊥AC、FD⊥AB,則下列結論不成立的是( )

A.△DEF是等邊三角形
B.△ADF≌△BED≌△CFE
C.DE=![]() AB
AB
D.S△ABC=3S△DEF
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在邊長為1個單位長度的小正方形組成的網格中,給出了格點△ABC(頂點是網格線的交點)和點A1.
(1)畫出一個格點△A1B1C1,并使它與△ABC全等且A與A1是對應點;
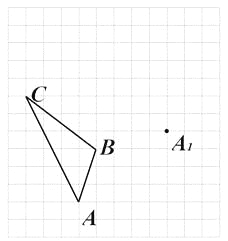
(2)畫出點B關于直線AC的對稱點D,并指出AD可以看作由AB繞A點經過怎樣的旋轉而得到的.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系內,拋物線![]() 與線段
與線段![]() 有兩個不同的交點,其中點
有兩個不同的交點,其中點![]() ,點
,點![]() .有下列結論:
.有下列結論:
①直線![]() 的解析式為
的解析式為![]() ;②方程
;②方程![]() 有兩個不相等的實數根;③a的取值范圍是
有兩個不相等的實數根;③a的取值范圍是![]() 或
或![]() .
.
其中,正確結論的個數為( )
A.0B.1C.2D.3
查看答案和解析>>
科目:初中數學 來源: 題型:
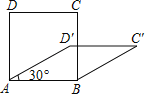
【題目】四邊形具有不穩定性,對于四條邊長確定的四邊形.當內角度數發生變化時,其形狀也會隨之改變.如圖,改變正方形ABCD的內角,正方形ABCD變為菱形ABC′D′.若∠D′AB=30°,則菱形ABC′D′的面積與正方形ABCD的面積之比是( )
A.1B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
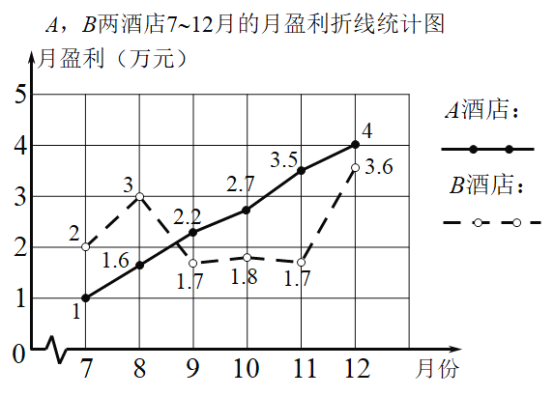
【題目】A,B兩家酒店規模相當,去年下半年的月盈利折線統計圖如圖所示.
(1)要評價這兩家酒店7~12月的月盈利的平均水平,你選擇什么統計量?求出這個統計量;
(2)已知A,B兩家酒店7~12月的月盈利的方差分別為1.073(平方萬元),0.54(平方萬元).根據所給的方差和你在(1)中所求的統計量,結合折線統計圖,你認為去年下半年哪家酒店經營狀況較好?請簡述理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com