
如圖所示,在平面直角坐標系xOy中,AB在x軸上,以AB為直徑的半⊙Oˊ與y軸正半軸交于點C,連接BC,AC。CD是半⊙Oˊ的切線,AD⊥CD于點D。

(1)求證:∠CAD =∠CAB;
(2)已知拋物線y=ax2+bx+c過A、B、C三點,AB=10,AC=2BC。
①求拋物線的解析式;
②判斷拋物線的頂點E是否在直線CD上,并說明理由。
(1)證明見解析;(2)y=-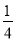 x2-
x2-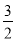 x+4;在,理由見解析.
x+4;在,理由見解析.
【解析】
試題分析:(1)連接O′C,由CD是⊙O的切線,可得O′C⊥CD,則可證得O′C∥AD,又由O′A=O′C,則可證得∠CAD=∠CAB;
(2)①首先證得△CAO∽△BCO,根據相似三角形的對應邊成比例,可得OC2=OA•OB,又由tan∠CAO=tan∠CAD=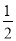 ,則可求得CO,AO,BO的長,然后利用待定系數法即可求得二次函數的解析式;
,則可求得CO,AO,BO的長,然后利用待定系數法即可求得二次函數的解析式;
②首先證得△FO′C∽△FAD,由相似三角形的對應邊成比例,即可得到F的坐標,求得直線DC的解析式,然后將拋物線的頂點坐標代入檢驗即可求得答案;
試題解析:(1)證明:連接O′C,
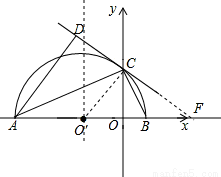
∵CD是⊙O′的切線,
∴O′C⊥CD,
∵AD⊥CD,
∴O′C∥AD,
∴∠O′CA=∠CAD,
∵O′A=O′C,
∴∠CAB=∠O′CA,
∴∠CAD=∠CAB;
(2)【解析】
①∵AB是⊙O′的直徑,
∴∠ACB=90°,
∵OC⊥AB,
∴∠CAB=∠OCB,
∴△CAO∽△BCO,
∴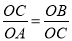 ,
,
即OC2=OA•OB,
∵tan∠CAO=tan∠CAD=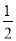 ,
,
∴AO=2CO,
又∵AB=10,
∴OC2=2CO(10-2CO),
解得CO1=4,CO2=0(舍去),
∴CO=4,AO=8,BO=2
∵CO>0,
∴CO=4,AO=8,BO=2,
∴A(-8,0),B(2,0),C(0,4),
∵拋物線y=ax2+bx+c過點A,B,C三點,
∴c=4,
由題意得: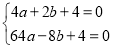 ,
,
解得: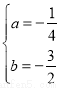 ,
,
∴拋物線的解析式為:y=-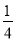 x2-
x2-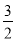 x+4;
x+4;
②設直線DC交x軸于點F,
∴△AOC≌△ADC,
∴AD=AO=8,
∵O′C∥AD,
∴△FO′C∽△FAD,
∴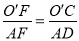 ,
,
∴O′F•AD=O′C•AF,
∴8(BF+5)=5(BF+10),
∴BF=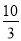 ,F(
,F(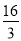 ,0);
,0);
設直線DC的解析式為y=kx+m,
則
 ,
,
解得: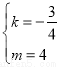 ,
,
∴直線DC的解析式為y=-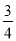 x+4,
x+4,
由y=-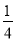 x2-
x2-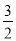 x+4=-
x+4=-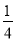 (x+3)2+
(x+3)2+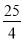 得頂點E的坐標為(-3,
得頂點E的坐標為(-3,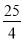 ),
),
將E(-3,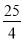 )代入直線DC的解析式y=-
)代入直線DC的解析式y=-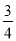 x+4中,
x+4中,
右邊=-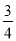 ×(-3)+4=
×(-3)+4=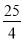 =左邊,
=左邊,
∴拋物線頂點E在直線CD上;
考點:二次函數綜合題.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源:2014-2015學年江蘇省蘇州市九年級12月月考數學試卷(解析版) 題型:選擇題
已知函數y=(x﹣m)(x﹣n)(其中m<n)的圖象如圖所示,則一次函數y=mx+n與反比例函數y=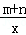 的圖象可能是( )
的圖象可能是( )
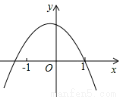
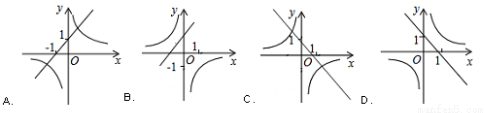
查看答案和解析>>
科目:初中數學 來源:2014-2015學年江蘇省九年級12月階段調研測試數學試卷(解析版) 題型:選擇題
一元二次方程x2 +2x+4=0的根的情況是( )
A.有兩個不相等的實數根
B.有兩個相等的實數根
C.沒有實數根
D.無法確定
查看答案和解析>>
科目:初中數學 來源:2014-2015學年廣西省九年級12月月考數學試卷(解析版) 題型:選擇題
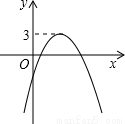
函數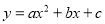 的圖像如圖所示,那么關于
的圖像如圖所示,那么關于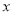 的方程
的方程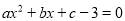 的根的情況是( )
的根的情況是( )
A.有兩個不相等的實數根 B.有兩個異號實數根
C.有兩個相等的實數根 D.無實數根
查看答案和解析>>
科目:初中數學 來源:2014-2015學年福建省龍巖市永定豐田片區九年級上學期第三次月考數學試卷(解析版) 題型:解答題
某地方政府出臺了一系列“三農”優惠政策,使農民收入大幅度增加。某農戶生產經銷一種農產品,已知這種產品的成本價為每千克20元,市場調查發現,該產品每天的銷售量y(千克)與銷售價x(元/千克)有如下關系:y=-2x+80。設這種產品每天的銷售利潤為W元。
(1)求W與x之間的函數關系式。
(2)該產品銷售價定為每千克多少元時,每天的銷售利潤最大?最大利潤是多少元?
(3)如果物價部門規定這種產品的銷售價不高于每千克28元,該農戶想要每天獲得150元的銷售利潤,銷售價應定為每千克多少元?
查看答案和解析>>
科目:初中數學 來源:2014-2015學年福建省龍巖市永定豐田片區九年級上學期第三次月考數學試卷(解析版) 題型:填空題
一個口袋里放有三枚除顏色外都相同的棋子,其中有兩枚是白色的,一枚是紅色的。從中隨機摸出一枚記下顏色,放回口袋攪勻,再從中隨機摸出一枚記下顏色,兩次摸出棋子顏色不同的概率是 。
查看答案和解析>>
科目:初中數學 來源:2013-2014學年云南省九年級11月月考數學試卷(解析版) 題型:解答題
已知關于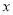 的方程
的方程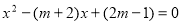 。
。
(1)求證:方程恒有兩個不相等的實數根。
(2)若此方程的一個根為1,請求出方程的另一個根,并求以此兩根為邊長的直角三角形的周長。
查看答案和解析>>
科目:初中數學 來源:2014-2015學年云南省七年級上學期期末考試數學試卷(解析版) 題型:選擇題
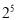 表示的意義是 ( )
表示的意義是 ( )
A.5個2相乘
B.5與2相乘
C.5個2相加
D.2個5相乘
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com