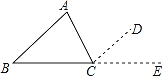
【題目】已知：△ABC，∠A、∠B、∠C之和為多少？為什么？
解：∠A+∠B+∠C=180°
理由：作∠ACD=∠A，并延長BC到E
∵∠ACD=∠ （已作）
AB∥CD（ ）
∴∠B= （ ）
而∠ACB+∠ACD+∠DCE=180°
∴∠ACB+ + =180°（ ）
口算能手系列答案科目：初中數學 來源： 題型：
【題目】2016年2月1日，我國在西昌衛星發射中心，用長征三號丙運載火箭成功將第5顆新一代北斗星送入預定軌道，如圖，火箭從地面L處發射，當火箭達到A點時，從位于地面R處雷達站測得AR的距離是6km，仰角為42.4°；1秒后火箭到達B點，此時測得仰角為45.5°
（1）求發射臺與雷達站之間的距離LR；
（2）求這枚火箭從A到B的平均速度是多少（結果精確到0.01）？
（參考數據：son42.4°≈0.67，cos42.4°≈0.74，tan42.4°≈0.905，sin45.5°≈0.71，cos45.5°≈0.70，tan45.5°≈1.02 ）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】為了解學生課外閱讀的喜好，某校從八年級隨機抽取部分學生進行問卷調查，調查要求每人只選取一種喜歡的書籍，如果沒有喜歡的書籍，則作“其它”類統計。圖（1）與圖（2）是整理數據后繪制的兩幅不完整的統計圖。以下結論不正確的是（ ）
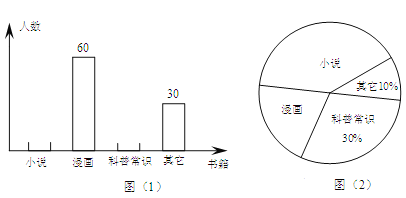
A. 由這兩個統計圖可知喜歡“科普常識”的學生有90人．
B. 若該年級共有1200名學生，則由這兩個統計圖可估計喜愛“科普常識”的學生約有360個．
C. 由這兩個統計圖不能確定喜歡“小說”的人數．
D. 在扇形統計圖中，“漫畫”所在扇形的圓心角為72°．
查看答案和解析>>
科目：初中數學 來源： 題型：
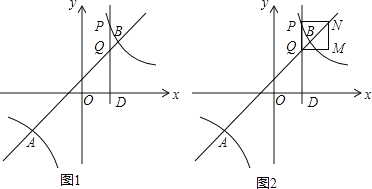
【題目】如圖，已知A(－4，n)、B(3，4)是一次函數y1＝kx＋b的圖象與反比例函數
的圖象的兩個交點，過點D(t，0)（0＜t＜3）作x軸的垂線，分別交雙曲線
和直線y1＝kx＋b于P、Q兩點
(1) 直接寫出反比例函數和一次函數的解析式
(2) 當t為何值時，S△BPQ＝
S△APQ
(3) 以PQ為邊在直線PQ的右側作正方形PQMN，試說明：邊QM與雙曲線
（x＞0）始終有交點
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知AM∥BN，∠A=80°，點P是射線AM上動點（與A不重合），BC、BD分別平分∠ABP和∠PBN，交射線AM于C、D．
（1）求∠CBD的度數；
（2）當點P運動時，那么∠APB：∠ADB的度數比值是否隨之發生變化？若不變，請求出這個比值；若變化，請找出變化規律；
（3）當點P運動到使∠ACB=∠ABD時，求∠ABC的度數．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】雙胞胎兄弟小明和小亮在同一班讀書，周五16：00時放學后，小明和同學走路回家，途中沒有停留，小亮騎車回家，他們各自與學校的距離s(米)與用去的時間t(分)的關系如圖所示，根據圖象提供的有關信息，下列說法中錯誤的是( )
A. 兄弟倆的家離學校1000米
B. 他們同時到家，用時30分
C. 小明的速度為50米/分
D. 小亮中間停留了一段時間后，再以80米/分的速度騎回家
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知∠1＝68°，∠2＝68°，∠3＝112°.在下列解答中，填空：
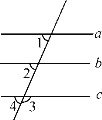
(1)因為∠1＝68°，∠2＝68°(已知)，
所以__________(等量代換)．
所以____∥_____________________________．
(2)因為∠3＋∠4＝180°(鄰補角的定義)，∠3＝112°
，所以____________
又因為∠2＝68°，
所以___________(等量代換)，
所以____∥_________________________________．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
