
【題目】如圖,四邊形ABCD的對(duì)角線AC、BD相交于點(diǎn)O,分別作BE⊥AC于E,DF⊥AC于F,已知OE=OF,CE=AF.

(1)求證:△BOE≌△DOF;
(2)若![]() ,則四邊形ABCD是什么特殊四邊形?請(qǐng)說明理由.
,則四邊形ABCD是什么特殊四邊形?請(qǐng)說明理由.
【答案】(1)證明見解析;(2)解:四邊形ABCD是矩形,理由見解析.
【解析】(1)根據(jù)AAS或ASA即可證明;(2)結(jié)論:矩形. 只要證明對(duì)角線AC=BD即可;
解: (1)∴ ∠BEO=90°=∠DFO ,
又∵ OE=OF ∠BOE=∠DOF,
∴ △BOE≌△DOF(ASA),
(2)解:四邊形ABCD是矩形,
證明:∵ △BOE≌△DOF,
∴ OB=OD,
∵ OE=OF,CE=AF,
∴ OC=OA,
∴ 四邊形ABCD是平行四邊形,
∴![]() ,
,
又∵![]() ,
,
∴ AC=BD,
∴□ABCD是矩形.
“點(diǎn)睛”本題考查全等三角形的判定與性質(zhì)、平行四邊形的判定和性質(zhì). 矩形的判定和性質(zhì)等知識(shí),解題的關(guān)鍵是熟練掌握基本概念,靈活運(yùn)用知識(shí)解決問題,屬于中考常考題型.


 名師伴你成長課時(shí)同步學(xué)練測(cè)系列答案
名師伴你成長課時(shí)同步學(xué)練測(cè)系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】一名同學(xué)調(diào)查了全班![]() 名同學(xué)分別喜歡相聲、小品、歌曲、舞蹈節(jié)目的類別情況,并制成如下統(tǒng)計(jì)表:
名同學(xué)分別喜歡相聲、小品、歌曲、舞蹈節(jié)目的類別情況,并制成如下統(tǒng)計(jì)表:
最喜歡的節(jié)目類別 | 劃記 | 人數(shù) | 百分?jǐn)?shù)(%) |
相聲 | 正 |
|
|
小品 | 正正正一 |
|
|
歌曲 | 正正 |
|
|
舞蹈 | 正一 |
|
|
其中對(duì)這些節(jié)目類別的統(tǒng)計(jì)中,僅有一類節(jié)目的統(tǒng)計(jì)是完全正確的,該項(xiàng)統(tǒng)計(jì)類別是( )
A.相聲B.小品C.歌曲D.舞蹈
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某學(xué)校準(zhǔn)備從體育用品商店一次性購買若干個(gè)籃球和足球(每個(gè)籃球的價(jià)格相同,每個(gè)足球的價(jià)格相同),購買1個(gè)足球和2個(gè)籃球共需270元;購買2個(gè)足球和3個(gè)籃球共需440元.
(1)問足球和籃球的單價(jià)各是多少元?
(2)若購買足球和籃球共24個(gè),且購買籃球的個(gè)數(shù)大于足球個(gè)數(shù)的2倍,購買球的總費(fèi)用不超過2220元,問該學(xué)校有哪幾種不同的購買方案?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】二次函數(shù)y=3x2+1和y=3(x﹣1)2 , 以下說法: ①它們的圖象都是開口向上;
②它們的對(duì)稱軸都是y軸,頂點(diǎn)坐標(biāo)都是原點(diǎn)(0,0);
③當(dāng)x>0時(shí),它們的函數(shù)值y都是隨著x的增大而增大;
④它們的開口的大小是一樣的.
其中正確的說法有( )
A. 1個(gè) B. 2 C. 3 D. 4個(gè)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖在平面直角坐標(biāo)系中,點(diǎn)![]() 坐標(biāo)
坐標(biāo)![]() ,點(diǎn)
,點(diǎn)![]() 坐標(biāo)
坐標(biāo)![]() ,連接
,連接![]() ,
,![]() 平分
平分![]() 交
交![]() 于點(diǎn)
于點(diǎn)![]() .
.
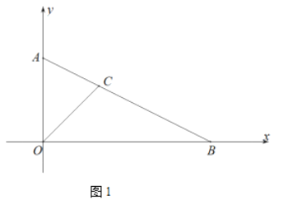
(1)如圖1,求![]() 的長;
的長;
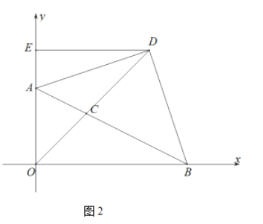
(2)如圖2,![]() 是
是![]() 延長線上一點(diǎn),連接
延長線上一點(diǎn),連接![]() ,
,![]() ,且
,且![]() ,過點(diǎn)
,過點(diǎn)![]() 作
作![]() 軸于點(diǎn)
軸于點(diǎn)![]() ,若點(diǎn)
,若點(diǎn)![]() 是線段
是線段![]() 上一點(diǎn),點(diǎn)
上一點(diǎn),點(diǎn)![]() 的橫坐標(biāo)為
的橫坐標(biāo)為![]() ,連接
,連接![]() ,設(shè)
,設(shè)![]() 的面積為
的面積為![]() ,求
,求![]() 與
與![]() 的關(guān)系;
的關(guān)系;
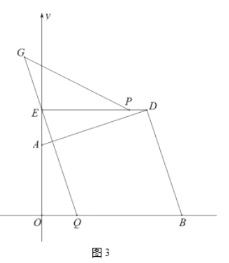
(3)在(2)的條件下,如圖3,線段![]() 上存在一點(diǎn)
上存在一點(diǎn)![]() ,使得
,使得![]() ,點(diǎn)
,點(diǎn)![]() 在
在![]() 的延長線上,且
的延長線上,且![]() ,連接
,連接![]() ,若
,若![]() ,求點(diǎn)
,求點(diǎn)![]() 的坐標(biāo)及
的坐標(biāo)及![]() 值?
值?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
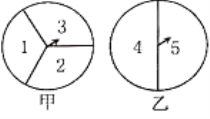
【題目】如圖,甲轉(zhuǎn)盤被分成3個(gè)面積相等的扇形、乙轉(zhuǎn)盤被分成2個(gè)面積相等的扇形.小夏和小秋利用它們來做決定獲勝與否的游戲.規(guī)定小夏轉(zhuǎn)甲盤一次、小秋轉(zhuǎn)乙盤一次為一次游戲(當(dāng)指針指在邊界線上時(shí)視為無效,重轉(zhuǎn)).
(1)小夏說:“如果兩個(gè)指針?biāo)竻^(qū)域內(nèi)的數(shù)之和為6或7,則我獲勝;否則你獲勝”.按小夏設(shè)計(jì)的規(guī)則,請(qǐng)你寫出兩人獲勝的可能性分別是多少?
(2)請(qǐng)你對(duì)小夏和小秋玩的這種游戲設(shè)計(jì)一種公平的游戲規(guī)則,并用一種合適的方法(例如:樹狀圖,列表)說明其公平性.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系![]() 中,已知點(diǎn)
中,已知點(diǎn)![]() ,
,![]() ,請(qǐng)確定點(diǎn)C的坐標(biāo),使得以A,B,C,O為頂點(diǎn)的四邊形是平行四邊形,則滿足條件的所有點(diǎn)C的坐標(biāo)是___________.
,請(qǐng)確定點(diǎn)C的坐標(biāo),使得以A,B,C,O為頂點(diǎn)的四邊形是平行四邊形,則滿足條件的所有點(diǎn)C的坐標(biāo)是___________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】“五一”期間,某商場(chǎng)搞優(yōu)惠促銷,決定由顧客抽獎(jiǎng)確定折扣.某顧客購買甲、乙兩種商品,分別抽到七折(按售價(jià)的70%銷售)和九折(按售價(jià)的90%銷售),共付款386元,這兩種商品原銷售價(jià)之和為500元.問:這兩種商品的原銷售價(jià)分別為多少元?
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com