
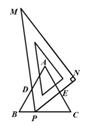
如圖,在等邊△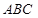 中,
中,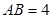 ,當直角三角板
,當直角三角板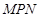 的
的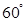 角的頂點
角的頂點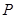 在
在 上移動時,斜邊
上移動時,斜邊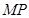 始終經過
始終經過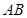 邊的中點
邊的中點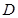 ,設直角三角板的另一直角邊
,設直角三角板的另一直角邊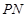 與
與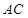 相交于點E.設
相交于點E.設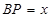 ,
,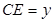 ,那么
,那么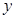 與
與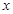 之間的函數圖象大致是( )
之間的函數圖象大致是( )
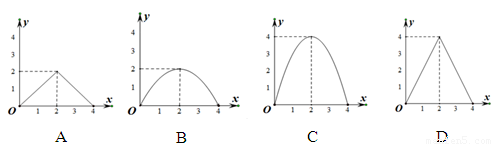
B.
【解析】
試題分析:根據等邊三角形的性質得BD=2,PC=4-x,∠B=∠C=60°,由于∠MPN=60°,易得∠DPB=∠PEC,根據三角形相似的判定方法得到△BPD∽△CEP,利用相似比即可得到y=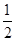 x(4-x),配方得到y=-
x(4-x),配方得到y=-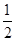 (x-2)2+2,然后根據二次函數的性質對各選項進行判斷.
(x-2)2+2,然后根據二次函數的性質對各選項進行判斷.
∵等邊△ABC中,AB=4,BP=x,
∴BD=2,PC=4-x,∠B=∠C=60°,
∵∠MPN=60°,
∴∠DPB+∠EPC=120°,
∵∠EPC+∠PEC=120°,
∴∠DPB=∠PEC,
∴△BPD∽△CEP,
∴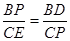 ,即
,即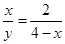 ,
,
∴y=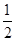 x(4-x)=-
x(4-x)=-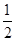 (x-2)2+2,(0≤x≤4).
(x-2)2+2,(0≤x≤4).
故選B.
考點: 動點問題的函數圖象.


科目:初中數學 來源: 題型:
 如圖,在等邊△ABC中,D、E、F分別是BC,AC,AB上的點,且DE⊥AC,EF⊥AB,FD⊥BC,則△DEF與△ABC的面積之比等于( )
如圖,在等邊△ABC中,D、E、F分別是BC,AC,AB上的點,且DE⊥AC,EF⊥AB,FD⊥BC,則△DEF與△ABC的面積之比等于( )| A、1:3 | ||
| B、2:3 | ||
C、
| ||
D、
|
查看答案和解析>>
科目:初中數學 來源: 題型:
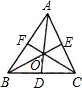 如圖,在等邊△ABC中,D、E、F是三邊中點.在圖中可以數出的三角形中,任選一對三角形(不計順序),如果這2個三角形至少有一條邊相等,便稱之為一對“友好三角形”.那么,從圖中選出“友好三角形”共有( )
如圖,在等邊△ABC中,D、E、F是三邊中點.在圖中可以數出的三角形中,任選一對三角形(不計順序),如果這2個三角形至少有一條邊相等,便稱之為一對“友好三角形”.那么,從圖中選出“友好三角形”共有( )| A、120對 | B、240對 | C、234對 | D、114對 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com