
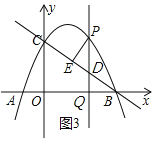
【題目】如圖,已知拋物線y=ax2+bx+c與x軸交于A(-1,0)、B(4,0)兩點,與y軸交于點C(0,2),
(1)求拋物線的函數表達式;
(2)如圖,在拋物線對稱軸上取兩個點G、H(G在H的上方),且滿足GH=1,連接CG,AH,求四邊形CGHA的周長的最小值;
(3)如圖,點P是拋物線第一象限的一個動點,過點P作PQ⊥x軸于點Q,交BC于點D,PE⊥BC于點E,設△PDE的面積為S,求當S取得最大值時點P的坐標,并求S的最大值.

【答案】(1)![]() (2)
(2)![]() +
+![]() +1.(3)點P的坐標為(2,3)時,S取最大值,最大值為
+1.(3)點P的坐標為(2,3)時,S取最大值,最大值為![]() .
.
【解析】
(1)由點A,B,C的坐標,利用待定系數法可求出拋物線的函數表達式;
(2)將拋物線的函數表達式變形為頂點式,可得出拋物線的對稱軸,在y軸上截取CC′=GH(點C′在點C的下方),連接BC′交拋物線對稱軸于點H,此時四邊形CGHA的周長取最小值,由點C的坐標結合GH=1可得出點C′的坐標,由點A,C,B,C′的坐標利用勾股定理可求出AC,BC′的長度,將其代入四邊形CGHA的周長的最小值=AC+BC′+GH中,即可求出結論;
(3)由點B,C的坐標,利用待定系數法可求出直線BC的函數表達式,設點P的坐標為(m,-![]() m2+
m2+![]() m+2)(0<m<4),則點D的坐標為(m,-
m+2)(0<m<4),則點D的坐標為(m,-![]() m+2),進而可得出PD的長度,由PE⊥BC,PQ⊥x軸及∠PDE=∠BDQ可得出∠DPE=∠DBQ,結合tan∠DPE=
m+2),進而可得出PD的長度,由PE⊥BC,PQ⊥x軸及∠PDE=∠BDQ可得出∠DPE=∠DBQ,結合tan∠DPE=![]() 可得出PE=2DE,PD=
可得出PE=2DE,PD=![]() DE,再利用三角形的面積公式可得出S=
DE,再利用三角形的面積公式可得出S=![]() PD2,由PD=-
PD2,由PD=-![]() m2+2m,利用二次函數的性質可求出PD的最大值,代入S=
m2+2m,利用二次函數的性質可求出PD的最大值,代入S=![]() PD2中即可求出S的最大值.
PD2中即可求出S的最大值.
(1)將A(-1,0),B(4,0),C(0,2)代入y=ax2+bx+c,得:
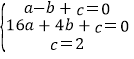 ,解得:
,解得: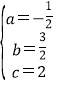 ,
,
∴拋物線的函數表達式為y=-![]() x2+
x2+![]() x+2.
x+2.
(2)∵y=-![]() x2+
x2+![]() x+2=-
x+2=-![]() (x-
(x-![]() )2+
)2+![]() ,
,
∴拋物線的對稱軸為直線x=![]() .
.
如圖2,在y軸上截取CC′=GH(點C′在點C的下方),連接BC′交拋物線對稱軸于點H.
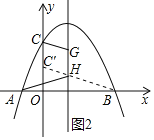
∵CC′∥GH,
∴四邊形CC′HG為平行四邊形,
∴C′H=CG.
又∵點A,B關于拋物線的對稱軸對稱,
∴BH=AH,
∴AH+CG=BH+C′H=BC′,即此時四邊形CGHA的周長取最小值.
∵點C的坐標為(0,2),GH=1,
∴點C′的坐標為(0,1).
∵點A的坐標為(-1,0),點B的坐標為(4,0),
∴AC=![]() =
=![]() ,BC′=
,BC′=![]() =
=![]() ,
,
∴四邊形CGHA的周長的最小值=AC+BC′+GH=![]() +
+![]() +1.
+1.
(3)設直線BC的函數表達式為y=kx+d(k≠0),
將B(4,0),C(0,2)代入y=kx+d,得:
![]() ,解得:
,解得: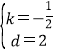 ,
,
∴直線BC的函數表達式為y=-![]() x+2.
x+2.
設點P的坐標為(m,-![]() m2+
m2+![]() m+2)(0<m<4),則點D的坐標為(m,-
m+2)(0<m<4),則點D的坐標為(m,-![]() m+2),
m+2),
∴PD=-![]() m2+
m2+![]() m+2-(-
m+2-(-![]() m+2)=-
m+2)=-![]() m2+2m.
m2+2m.
∵PE⊥BC,PQ⊥x軸,
∴∠PED=∠BQD=90°.
∵∠PDE=∠BDQ,
∴∠DPE=∠DBQ,
∴tan∠DPE=![]() ,
,
∴PE=2DE,PD=![]() DE,
DE,
∴S=![]() DEPE=
DEPE=![]() ×
×![]() PD×
PD×![]() PD=
PD=![]() PD2.
PD2.
∵在PD=-![]() m2+2m=-
m2+2m=-![]() (m-2)2+2中,-
(m-2)2+2中,-![]() <0,
<0,
∴當m=2時,PD取最大值,最大值為2,
∴當點P的坐標為(2,3)時,S取最大值,最大值為![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】為響應市委、市政府創建“森林城市”的號召,某中學在校園內計劃種植柳樹和銀杏樹.已知購買2棵柳樹苗和3棵銀杏樹苗共需1800元,購買4棵柳樹苗和1棵銀杏樹苗共需1100元.
(1)求每棵柳樹苗和每棵銀杏樹苗各多少錢?
(2)該校計劃購買兩種樹苗共100棵,并且銀杏樹苗的數量不少于柳樹苗的![]() ,請設計出最省錢的購買方案,并說明理由.
,請設計出最省錢的購買方案,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在三個完全相同的小球上分別寫上-2,-1,2三個數字,然后裝入一個不透明的布袋內攪勻,從布袋中取出一個球,記下小球上的數字為![]() ,放回袋中再攪勻,然后再從袋中取出一個小球,記下小球上的數字為
,放回袋中再攪勻,然后再從袋中取出一個小球,記下小球上的數字為![]() ,組成一對數
,組成一對數![]() .
.
(1)請用列表或畫樹狀圖的方法,表示出數對![]() 的所有可能的結果;
的所有可能的結果;
(2)求直線![]() 不經過第一象限的概率.
不經過第一象限的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
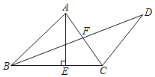
【題目】如圖,△ABC中,AE⊥BC于E,點D在∠ABC的平分線上,AC與BD交于F,連CD,∠ACD+2∠ACB=180°,AB=2EC,BD=2![]() ,BE=3,則AF=______.
,BE=3,則AF=______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】不透明的口袋里裝有紅、黃、藍三種顏色的小球若干個(除顏色外其余都相同),其中紅球2個(分別標有1號、2號),藍球1個.若從中任意摸出一個球,它是藍球的概率為![]() .
.
(1)求袋中黃球的個數;
(2)從袋中一次摸出兩個球,請用畫樹狀圖或列表格的方法列出所有等可能的結果,并求出摸到兩個不同顏色球的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
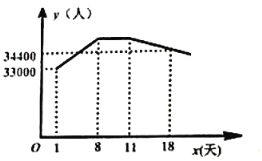
【題目】某市植物園于2019年3月-5月舉辦花展,按照往年的規律推算,自4月下旬起游客量每天增加![]() 人,游客量預計將在5月1日達到高峰,并持續到5月4日,隨后游客量每天有所減少.已知4月24日為第一天起,每天的游客量
人,游客量預計將在5月1日達到高峰,并持續到5月4日,隨后游客量每天有所減少.已知4月24日為第一天起,每天的游客量![]() (人)與時間
(人)與時間![]() (天)的函數圖像如圖所示,結合圖像提供的信息,解答下列問題:
(天)的函數圖像如圖所示,結合圖像提供的信息,解答下列問題:
![]() 已知該植物園門票
已知該植物園門票![]() 元/張,若每位游客在園內每天平均消費
元/張,若每位游客在園內每天平均消費![]() 元,試求5月1日-5月4日,所有游客消費總額為多少元?
元,試求5月1日-5月4日,所有游客消費總額為多少元?
![]() 當
當![]() 時,求
時,求![]() 關于
關于![]() 的函數解析式.
的函數解析式.
查看答案和解析>>
科目:初中數學 來源: 題型:
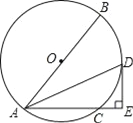
【題目】如圖,已知⊙O的直徑AB=10,弦AC=6,∠BAC的平分線交⊙O于點D,過點D作DE⊥AC交AC的延長線于點E.
(1)求證:DE是⊙O的切線.
(2)求DE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(探究)(1)觀察下列算式,并完成填空:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
……
![]() .(
.(![]() 是正整數)
是正整數)
(2)某市一廣場用正六邊形、正方形和正三角形地板磚鋪設圖案,圖案中央是一塊正六邊形地板磚,周圍是正方形和正三角形的地板磚,從里向外第一層包括6塊正方形和6塊正三角形地板磚;第二層包括6塊正方形和18塊正三角形地板磚;以此遞推.
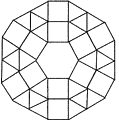
①第3層中分別含有______塊正方形和______塊正三角形地板磚;
②第![]() 層中含有______塊正三角形地板磚(用含
層中含有______塊正三角形地板磚(用含![]() 的代數式表示).
的代數式表示).
(應用)
該市打算在一個新建廣場中央,也采用這個樣式的圖案鋪設地面,現有1塊正六邊形、150塊正方形和420塊正三角形地板磚,問:鋪設這樣的圖案,最多能鋪多少層?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點A1、A2、A3…在直線y=x上,點C1,C2,C3…在直線y=2x上,以它們為頂點依次構造第一個正方形A1C1A2B1,第二個正方形A2C2A3B2…,若A2的橫坐標是1,則B3的坐標是_____,第n個正方形的面積是_____.
[Failed to download image : http://192.168.0.10:8086/QBM/2019/5/21/2208296361205760/2209339150704640/STEM/947823175bfc4b878475a9a15e16a258.png]
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com