已知拋物線L:y=x2-(k-2)x+(k+1)2
(1)證明:不論k取何值,拋物線L的頂點C總在拋物線y=3x2+12x+9上;
(2)已知-4<k<0時,拋物線L和x軸有兩個不同的交點A、B,求A、B間距取得最大值時k的值;
(3)在(2)A、B間距取得最大值條件下(點A在點B的右側),直線y=ax+b是經過點A,且與拋物線L相交于點D的直線.問是否存在點D,使△ABD為等邊三角形?如果存在,請寫出此時直線AD的解析式;如果不存在,請說明理由.
【答案】
分析:(1)先求出拋物線的頂點坐標,然后代入函數解析式中,根據左右兩邊相等即可作出證明.
(2)設A(x
1,0),B(x
2,0),x
1>x
2,利用求根公式得出兩根的表達式,繼而表示出AB的長,然后可計算出最大值.
(3)若△ABD為等邊三角形,那么點D必在拋物線的對稱軸上,即只有拋物線的頂點才有可能符合D點的條件.首先,根據(2)的結果求出A、B、D三點坐標,根據這三點坐標特點判斷一下△ABD是否符合等邊三角形的特征,若符合,再根據待定系數法求出直線AD的解析式.
解答:解:(1)拋物線L的頂點坐標C是(
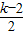
,
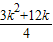
),
將頂點坐標C代入y=3x
2+12x+9,
左邊=
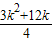
,右邊=3(
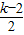
)
2+12(
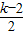
)+9=
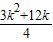
,
故可得:左邊=右邊,
所以無論k取何值,拋物線L的頂點C總在拋物線y=3x
2+12x+9上;
(2)已知-4<k<0時,拋物線L和x軸有兩個不同的交點A、B,
設A(x
1,0),B(x
2,0),x
1>x
2,
依題意x
1,2=
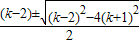
,
|AB|=|x
1-x
2|=|
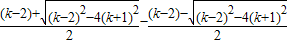
|
=
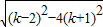
=
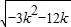
=
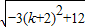
,
由此可知,當k=-2時,AB達到最大值
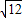
即2
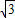
,
而k=-2恰好在-4<k<0內,
所以A、B間距取得最大值時k的值為-2.
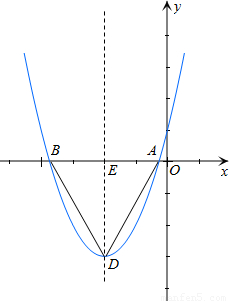
(3)存在.
因為若△ABD是等邊三角形,則點D應在線段AB的垂直平分線上,即在此拋物線的對稱軸上,
又∵點D在拋物線上,
∴若滿足條件的D存在,點D應是此拋物線的頂點,
當k=-2時,拋物線L:y=x
2+4x+1,頂點D(-2,-3),
解方程x
2+4x+1=0,得x
1=-2+
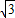
,x
2=-2-
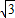
,
所以A(-2+
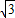
,0),B(-2-
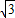
,0),
如圖,在△ABD中,DB=DA,
E為AB中點,AB=|(-2+
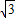
)-(-2-
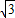
)|=2
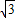
,
∴AE=
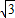
,tan∠BAD=
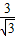
=
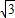
,
∴∠BAD=60°,
∴△ABD為等邊三角形,
因為直線y=ax+b經過點A(-2+
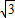
,0)、D(-2,-3),
所以依題意把k=2代入
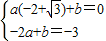
,
解得:
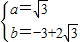
,
所以所求為y=
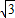
x-3+2
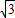
.
點評:該題考查了二次函數綜合題,其中的知識點有:函數解析式的確定、根與系數的關系、等邊三角形的性質等知識;掌握二次函數與方程的關系以及拋物線的對稱性是解答此題的關鍵.

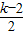 ,
,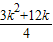 ),
),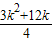 ,右邊=3(
,右邊=3(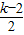 )2+12(
)2+12(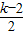 )+9=
)+9=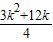 ,
,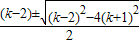 ,
,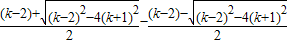 |
|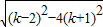 =
=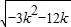 =
=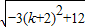 ,
,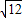 即2
即2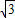 ,
,
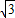 ,x2=-2-
,x2=-2-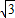 ,
,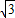 ,0),B(-2-
,0),B(-2-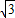 ,0),
,0),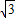 )-(-2-
)-(-2-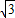 )|=2
)|=2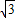 ,
,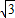 ,tan∠BAD=
,tan∠BAD=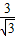 =
=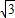 ,
,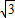 ,0)、D(-2,-3),
,0)、D(-2,-3),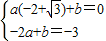 ,
,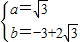 ,
,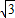 x-3+2
x-3+2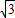 .
.

 閱讀快車系列答案
閱讀快車系列答案 正半軸交于點C.如果x1、x2是方程x2-x-6=0的兩個根(x1<x2),且△ABC的面積為
正半軸交于點C.如果x1、x2是方程x2-x-6=0的兩個根(x1<x2),且△ABC的面積為 廊橋是我國古老的文化遺產.如圖,是某座拋物線型的廊橋示意圖,已知拋物線的函數表達式為y=-
廊橋是我國古老的文化遺產.如圖,是某座拋物線型的廊橋示意圖,已知拋物線的函數表達式為y=-