
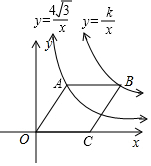
 如圖,點(diǎn)A在雙曲線y=$\frac{4\sqrt{3}}{x}$(x>0)上,點(diǎn)B在雙曲線y=$\frac{k}{x}$上,(點(diǎn)B在點(diǎn)A的右側(cè)),且AB∥x軸,若四邊形OABC是菱形,且∠AOC=60°,則k=12$\sqrt{3}$.
如圖,點(diǎn)A在雙曲線y=$\frac{4\sqrt{3}}{x}$(x>0)上,點(diǎn)B在雙曲線y=$\frac{k}{x}$上,(點(diǎn)B在點(diǎn)A的右側(cè)),且AB∥x軸,若四邊形OABC是菱形,且∠AOC=60°,則k=12$\sqrt{3}$. 分析 過(guò)點(diǎn)A作AD⊥x軸于點(diǎn)D,設(shè)OA的長(zhǎng)度為a,則點(diǎn)A的坐標(biāo)為($\frac{1}{2}$a,$\frac{\sqrt{3}}{2}$a),由點(diǎn)A在雙曲線y=$\frac{4\sqrt{3}}{x}$(x>0)上,即可求出a值,再根據(jù)菱形的性質(zhì)即可得出點(diǎn)C、B的坐標(biāo),由點(diǎn)B的坐標(biāo)利用反比例函數(shù)圖象上點(diǎn)的坐標(biāo)特征即可求出k值,此題得解.
解答 解:過(guò)點(diǎn)A作AD⊥x軸于點(diǎn)D,如圖所示.
設(shè)OA的長(zhǎng)度為a,則點(diǎn)A的坐標(biāo)為($\frac{1}{2}$a,$\frac{\sqrt{3}}{2}$a),
∵點(diǎn)A在雙曲線y=$\frac{4\sqrt{3}}{x}$(x>0)上,
∴$\frac{1}{2}$a•$\frac{\sqrt{3}}{2}$a=4$\sqrt{3}$,
∴a=4或a=-4(舍去),
∴點(diǎn)A(2,2$\sqrt{3}$).
∵四邊形OABC是菱形,
∴點(diǎn)C(4,0),
∵點(diǎn)O(0,0),
∴點(diǎn)B(6,2$\sqrt{3}$).
∵點(diǎn)B在雙曲線y=$\frac{k}{x}$上,
∴k=6×2$\sqrt{3}$=12$\sqrt{3}$.
故答案為:=12$\sqrt{3}$.
點(diǎn)評(píng) 本題考查了反比例函數(shù)圖象上點(diǎn)的坐標(biāo)特征以及菱形的性質(zhì),根據(jù)菱形的性質(zhì)找出點(diǎn)A、B的坐標(biāo)是解題的關(guān)鍵.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:選擇題
 如圖,設(shè)四邊形ABCD是邊長(zhǎng)為1的正方形,以對(duì)角線AC為邊作第2個(gè)正方形ACEF,再以對(duì)角線AE為邊作第3個(gè)正方形AEGH,如此下去…,記正方形ABCD的面積S1=1,按上述方法所作的正方形的面積依次為S2,S3…,Sn,則Sn=( )
如圖,設(shè)四邊形ABCD是邊長(zhǎng)為1的正方形,以對(duì)角線AC為邊作第2個(gè)正方形ACEF,再以對(duì)角線AE為邊作第3個(gè)正方形AEGH,如此下去…,記正方形ABCD的面積S1=1,按上述方法所作的正方形的面積依次為S2,S3…,Sn,則Sn=( )| A. | 2n-1 | B. | 2n | C. | 2n+1 | D. | 2n+2 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:選擇題
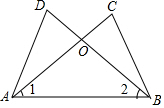 如圖,AC、BD相交于點(diǎn)O,∠1=∠2,若用“SAS”說(shuō)明△ACB≌△BDA,則還需要加上條件( )
如圖,AC、BD相交于點(diǎn)O,∠1=∠2,若用“SAS”說(shuō)明△ACB≌△BDA,則還需要加上條件( )| A. | AD=BC | B. | BD=AC | C. | ∠D=∠C | D. | OA=AB |
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | -3 | B. | -1 | C. | 1 | D. | 3 |
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com