
【題目】如圖,![]() 是路邊坡角為30°,長為10米的一道斜坡,在坡頂燈桿
是路邊坡角為30°,長為10米的一道斜坡,在坡頂燈桿![]() 的頂端
的頂端![]() 處有一探射燈,射出的邊緣光線
處有一探射燈,射出的邊緣光線![]() 和
和![]() 與水平路面
與水平路面![]() 所成的夾角
所成的夾角![]() 和
和![]() 分別是37°和60°(圖中的點
分別是37°和60°(圖中的點![]() 均在同一平面內,
均在同一平面內,![]() ).則
).則![]() 的長度約為( )(結果精確到0.1米,)參考數據:(
的長度約為( )(結果精確到0.1米,)參考數據:(![]() =1.73.sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
=1.73.sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
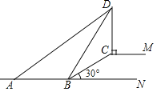
A. 9.4米B. 10.6米C. 11.4米D. 12.6米
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線 y1=﹣2x2+2,直線 y2=2x+2,當 x 任取一值時,x 對應的函數值分別為 y1、y2.若 y1≠y2,取 y1、y2 中的較小值記為 M;若 y1=y2,記 M=y1=y2.例如;當 x=1 時,y1=0,y2=4,y1<y2, 此時 M=0,下列判斷中正確的是( )

①當 x>0 時,y1>y2;②當 x<0 時,x 值越大,M 值越小;③使得 M 大于 2 的 x 值不存在;④使得 M=1 的 x 值是﹣![]() 或
或![]() .
.
A. ①②③ B. ①④ C. ②③④ D. ③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】楊輝是我國南宋時期杰出的數學家和教育家,如圖是楊輝在公元1261年的著作《詳解九章算法》里面的一張圖,即“楊輝三角”,該圖中有很多規律,請仔細觀察,解答下列問題:
(1)圖中給出了七行數字,根據構成規律,第![]() 行中從左邊數第
行中從左邊數第![]() 個數是 ;
個數是 ;
(2)第![]() 行中從左邊數第
行中從左邊數第![]() 個數為 ;第
個數為 ;第![]() 行中所有數字之和為 .
行中所有數字之和為 .

查看答案和解析>>
科目:初中數學 來源: 題型:
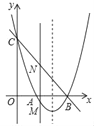
【題目】如圖,拋物線y=x2+bx+c與x軸交于點A和B(3,0),與y軸交于點C(0,3).
(1)求拋物線的解析式;
(2)若點M是拋物線上在x軸下方的動點,過M作MN∥y軸交直線BC于點N,求線段MN的最大值;
(3)E是拋物線對稱軸上一點,F是拋物線上一點,是否存在以A,B,E,F為頂點的四邊形是平行四邊形?若存在,請直接寫出點F的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一位小朋友在粗糙不打滑的“![]() ”字形平面軌道上滾動一個半徑為
”字形平面軌道上滾動一個半徑為![]() 的圓盤,如圖所示,
的圓盤,如圖所示,![]() 與
與![]() 是水平的,
是水平的,![]() 與水平面的夾角為
與水平面的夾角為![]() ,其中
,其中![]() ,
,![]() ,
,![]() .
.
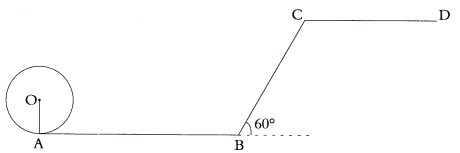
(1)小朋友將圓盤從點![]() 滾到與
滾到與![]() 相切的位置,此時圓盤的圓心
相切的位置,此時圓盤的圓心![]() 所經過的路線長為__________
所經過的路線長為__________![]() ;
;
(2)小朋友將圓盤從點![]() 滾動到點
滾動到點![]() ,其圓心所經過的路線長為__________
,其圓心所經過的路線長為__________![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
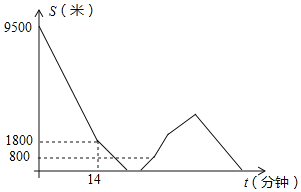
【題目】松松和東東騎自行車分別從迎賓大道上相距9500米的A、B兩地同時出發,相向而行,行駛一段時間后松松的自行車壞了,立刻停車并馬上打電話通知東東,東東接到電話后立刻提速至原來的![]() 倍,碰到松松后用了5分鐘修好了松松的自行車,修好車后東東立刻騎車以提速后的速度繼續向終點A地前行,松松則留在原地整理工具,2分鐘以后松松以原速向B走了3分鐘后,發現東東的包在自己身上,馬上掉頭以原速的
倍,碰到松松后用了5分鐘修好了松松的自行車,修好車后東東立刻騎車以提速后的速度繼續向終點A地前行,松松則留在原地整理工具,2分鐘以后松松以原速向B走了3分鐘后,發現東東的包在自己身上,馬上掉頭以原速的![]() 倍的速度回A地;在整個行駛過程中,松松和東東均保持勻速行駛(東東停車和打電話的時間忽略不計),兩人相距的路程S(米)與松松出發的時間t(分鐘)之間的關系如圖所示,則東東到達A地時,松松與A地的距離為_________米.
倍的速度回A地;在整個行駛過程中,松松和東東均保持勻速行駛(東東停車和打電話的時間忽略不計),兩人相距的路程S(米)與松松出發的時間t(分鐘)之間的關系如圖所示,則東東到達A地時,松松與A地的距離為_________米.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】若一個三位數的十位數字比個位數字和百位數字都大,則稱這個數為“傘數”.現從1,2,3,4這四個數字中任取3個數,組成無重復數字的三位數.
(1)請畫出樹狀圖并寫出所有可能得到的三位數;
(2)甲、乙二人玩一個游戲,游戲規則是:若組成的三位數是“傘數”,則甲勝;否則乙勝.你認為這個游戲公平嗎?試說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知![]() ,
,![]() ,
,![]() ,斜邊
,斜邊![]() ,將
,將![]() 繞點
繞點![]() 順時針旋轉
順時針旋轉![]() ,連接
,連接![]() .
.
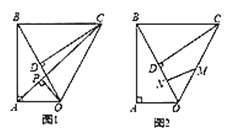
(1)如圖,連接![]() ,作
,作![]() ,垂足為
,垂足為![]() ,求
,求![]() 的面積和線段
的面積和線段![]() 的長;
的長;
(2)如圖,點![]() 是線段
是線段![]() 的中點,點
的中點,點![]() 是線段
是線段![]() 上的動點(不與點
上的動點(不與點![]() 重合),求
重合),求![]() 周長的最小值.
周長的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com