
| 1 | 2 | 3 | |
| 1 | 1 | 2 | 3 |
| 2 | 2 | 4 | 6 |
 .
. ,而積為奇數的有2種情況,概率是
,而積為奇數的有2種情況,概率是  ,獲勝的概率是不相等的.
,獲勝的概率是不相等的.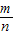 ,注意本題是放回實驗.解決本題的關鍵是得到相應的概率,概率相等就公平,否則就不公平.
,注意本題是放回實驗.解決本題的關鍵是得到相應的概率,概率相等就公平,否則就不公平. 

 教育世家狀元卷系列答案
教育世家狀元卷系列答案 黃岡課堂作業本系列答案
黃岡課堂作業本系列答案 單元加期末復習先鋒大考卷系列答案
單元加期末復習先鋒大考卷系列答案科目:初中數學 來源: 題型:
查看答案和解析>>
科目:初中數學 來源: 題型:
查看答案和解析>>
科目:初中數學 來源: 題型:
| 1 | 2 |
查看答案和解析>>
科目:初中數學 來源: 題型:
查看答案和解析>>
科目:初中數學 來源: 題型:
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com