
【題目】把邊長分別為4和6的矩形ABCO如圖放在平面直角坐標系中,將它繞點C順時針旋轉a角,旋轉后的矩形記為矩形EDCF.在旋轉過程中,
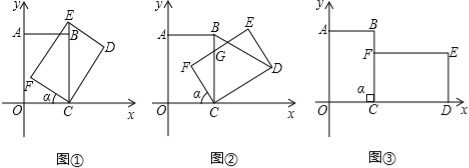
(1)如圖①,當點E在射線CB上時,E點坐標為 ;
(2)當△CBD是等邊三角形時,旋轉角a的度數是 (a為銳角時);
(3)如圖②,設EF與BC交于點G,當EG=CG時,求點G的坐標;
(4)如圖③,當旋轉角a=90°時,請判斷矩形EDCF的對稱中心H是否在以C為頂點,且經過點A的拋物線上.
【答案】(1)E(4,2![]() );
);
(2)60°;
(3)![]() ;
;
(4)點H不在此拋物線上.
【解析】
試題(1)依題意得點E在射線CB上,橫坐標為4,縱坐標根據勾股定理可得點E.
(2)已知∠BCD=60°,∠BCF=30°,然后可得∠α=60°.
(3)設CG=x,則EG=x,FG=6﹣x,根據勾股定理求出CG的值.
(4)設以C為頂點的拋物線的解析式為y=a(x﹣4)2,把點A的坐標代入求出a值.當x=7時代入函數解析式可得解.
解.(1)E(4,2![]() )
)
(2)60°
(3)設CG=x,則EG=x,FG=6﹣x,
在Rt△FGC中,∵CF2+FG2=CG2,
∴42+(6﹣x)2=x2
解得![]() ,即
,即![]()
∴![]()
(4)設以C為頂點的拋物線的解析式為y=a(x﹣4)2,
把A(0,6)代入,得6=a(0﹣4)2.
解得a=![]() .
.
∴拋物線的解析式為y=![]() (x﹣4)2
(x﹣4)2
∵矩形EDCF的對稱中心H即為對角線FD、CE的交點,
∴H(7,2).
當x=7時,![]()
∴點H不在此拋物線上.


 同步練習強化拓展系列答案
同步練習強化拓展系列答案科目:初中數學 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,點
,點![]() 從點
從點![]() 開始沿
開始沿![]() 邊向點
邊向點![]() 以
以![]() 的速度移動,點
的速度移動,點![]() 從點
從點![]() 開始沿
開始沿![]() 邊向點
邊向點![]() 以2
以2![]() 的速度移動.
的速度移動.
(1)如果點![]() ,
,![]() 分別從點
分別從點![]() ,
,![]() 同時出發,那么幾秒后,
同時出發,那么幾秒后,![]() 的面積等于6
的面積等于6![]() ?
?
(2)如果點![]() ,
,![]() 分別從點
分別從點![]() ,
,![]() 同時出發,那么幾秒后,
同時出發,那么幾秒后,![]() 的長度等于7
的長度等于7![]() ?
?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在等腰![]() 中,
中,![]() ,D為BC的中點,過點C作
,D為BC的中點,過點C作![]() 于點G,過點B作
于點G,過點B作![]() 于點B,交CG的延長線于點F,連接DF交AB于點E.
于點B,交CG的延長線于點F,連接DF交AB于點E.
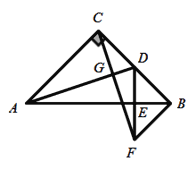
(1)求證:![]() ;
;
(2)求證:AB垂直平分DF;
(3)連接AF,試判斷![]() 的形狀,并說明理由.
的形狀,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
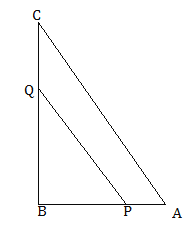
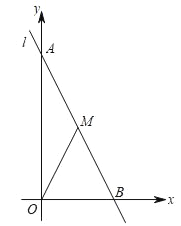
【題目】如圖,已知在平面直角坐標中,直線l:y=﹣2x+6分別交兩坐標于A、B兩點,M是級段AB上一個動點,設點M的橫坐標為x,△OMB的面積為S.
(1)寫出S與x的函數關系式;
(2)當△OMB的面積是△OAB面積的![]() 時,求點M的坐標;
時,求點M的坐標;
(3)當△OMB是以OB為底的等腰三角形,求它的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,某倉儲中心有一斜坡AB,其坡比為i=1∶2,頂部A處的高AC為4 m,B,C在同一水平面上.
(1)求斜坡AB的水平寬度BC;
(2)矩形DEFG為長方形貨柜的側面圖,其中DE=2.5 m,EF=2 m.將貨柜沿斜坡向上運送,當BF=3.5 m時,求點D離地面的高.(![]() ≈2.236,結果精確到0.1 m)
≈2.236,結果精確到0.1 m)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,BD是邊長為1的正方形ABCD的對角線,BE平分∠DBC交DC于點E,延長BC到點F,使CF=CE,連接DF,交BE的延長線于點G.
(1)求證:△BCE≌△DCF;
(2)求CF的長。

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com