
【題目】如圖,坡AB的坡度為1:2.4,坡面長26米,BC⊥AC,現(xiàn)計劃在斜坡中點D處挖去部分坡體(用陰影表示)修建一個平行于水平線CA的平臺DE和一條新的斜坡BE(請將下面兩小題的結果都精確到0.1米,參考數據:![]() ≈1.732).
≈1.732).
(1)若修建的斜坡BE的坡角(即∠BEF)恰為45°,則此時平臺DE的長為 米;
(2)坡前有一建筑物GH,小明在D點測得建筑物頂部H的仰角為30°,在坡底A點測得建筑物頂部H的仰角為60°,點B、C、A、G、H在同一平面內,點C、A、G在同一條水平直線上,問建筑物GH高為多少米?
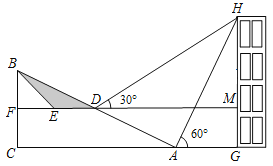
【答案】(1)7;(2)建筑物GH高約為17.9米.
【解析】
(1)由勾股定理分別求出BC,AC的長,再證明DF是△ABC的中位線,求出DF、BF的長,即可得出答案;
(2)過點D作DP⊥AC,垂足為P,解直角三角形即可得到結論.
解:(1)∵坡AB的坡度為1:2.4,坡面長26米,
設BC=x米,則AC=2.4x米,
由![]() ,得
,得 ![]()
解得,x=10,或x=-10(舍去)
∴BC=10,AC=24,
∵修建的斜坡BE的坡角∠BEF=45°,D為AB的中點,
∴AD=BD=13,
∵DF//AC,
∴DF為△ABC的中位線,
∴BF=CF=EF=![]() BC=5,DF=
BC=5,DF=![]() AC=12,
AC=12,
故:DE=DF﹣EF=12﹣5=7(米);
則平臺DE的長為7m,
故答案為:7;
(2)過點D作DP⊥AC,垂足為P.
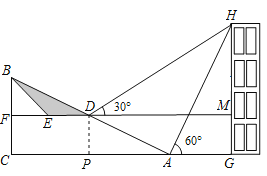
在Rt△DPA中,DP=CF=5,
PA=![]() AC=12,
AC=12,
在矩形DPGM中,MG=DP=12,DM=PG=12+AG,
在Rt△DMH中,
HM=DMtan30°=![]() ×(12+AG),
×(12+AG),
GH=HM+MG=![]() ×(12+AG)+5,
×(12+AG)+5,
∵∠HAG=60°,
∴tan60°=![]() =
=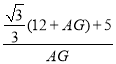 =
=![]() ,
,
解得:AG=![]() ,
,
∴HG=![]() AG=
AG=![]() ≈17.9(米),
≈17.9(米),
答:建筑物GH高約為17.9米.
【點題】
此題主要考查了解直角三角形中坡角問題,根據圖象構建直角三角形,進而利用銳角三角函數得出是解題關鍵.


科目:初中數學 來源: 題型:
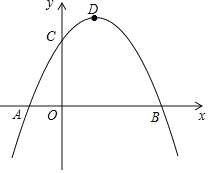
【題目】如圖,已知拋物線交x軸于A、B兩點,交y軸于C點,A點坐標為(﹣1,0),OC=2,OB=3,點D為拋物線的頂點.
(1)求拋物線的解析式;
(2)P為坐標平面內一點,以B、C、D、P為頂點的四邊形是平行四邊形,求P點坐標;
(3)若拋物線上有且僅有三個點M1、M2、M3使得△M1BC、△M2BC、△M3BC的面積均為定值S,求出定值S及M1、M2、M3這三個點的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】受新型冠狀病毒肺炎影響,學校開學時間延遲,為了保證學生停課不停學,某校開始實施網上教學,張老師統(tǒng)計了本班學生一周網上上課的時間(單位:分鐘)如下:200,180,150,200,250.關于這組數據,下列說法正確的是( )
A.中位數是200B.眾數是150C.平均數是190D.方差為0
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】春節(jié)前,安徽黃山腳下的小村莊的集市上,人山人海,還有人在擺“摸彩”游戲,只見他手拿一個黑色的袋子,內裝大小、形狀、質量完全相同的白球20只,且每一個球上都寫有號碼(1~20號)和1只紅球,規(guī)定:每次只摸一只球.摸前交1元錢且在1~20內寫一個號碼,摸到紅球獎5元,摸到號碼數與你寫的號碼相同獎10元.
(1)你認為該游戲對“摸彩”者有利嗎?說明你的理由.
(2)若一個“摸彩”者多次摸獎后,他平均每次將獲利或損失多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,點![]() 在拋物線上,將拋物線
在拋物線上,將拋物線![]() 在點
在點![]() 右側的部分沿著直線
右側的部分沿著直線![]() 翻折,翻折后的圖象與原拋物線剩余部分合稱為圖象
翻折,翻折后的圖象與原拋物線剩余部分合稱為圖象![]() .
.
(1)當![]() 時,
時,
①在如圖的平面直角坐標系中畫出圖象![]() ;
;
②直接寫出圖象![]() 對應函數的表達式;
對應函數的表達式;
③當![]() 時,圖象
時,圖象![]() 對應函數的最小值為
對應函數的最小值為![]() 求
求![]() 的取值范圍.
的取值范圍.
(2)當![]() 時,直接寫出圖象
時,直接寫出圖象![]() 對應函數
對應函數![]() 隨
隨![]() 增大而減小時
增大而減小時![]() 的取值范圍.
的取值范圍.
(3)若圖象![]() 上有且只有三個點到直線
上有且只有三個點到直線![]() 的距離為
的距離為![]() ,直接寫出
,直接寫出![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一次函數y=kx+b的圖象與反比例函數y=![]() 的圖象相交于A(-1,n),B(2,-1)兩點,與y軸相交于點C.
的圖象相交于A(-1,n),B(2,-1)兩點,與y軸相交于點C.
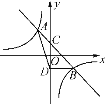
(1)求一次函數與反比例函數的表達式;
(2)若點D與點C關于x軸對稱,求△ABD的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在近期“抗疫”期間,某藥店銷售![]() 兩種型號的口罩,已知銷售
兩種型號的口罩,已知銷售![]() 只
只![]() 型和
型和![]() 只
只![]() 型的利潤為
型的利潤為![]() 元,銷售
元,銷售![]() 只
只![]() 型和
型和![]() 只
只![]() 型的利潤為
型的利潤為![]() 元.
元.
(1)求每只![]() 型口罩和
型口罩和![]() 型口罩的銷售利潤;
型口罩的銷售利潤;
(2)該藥店計劃一次購進兩種型號的口罩共![]() 只,其中
只,其中![]() 型口罩的進貨量不超過
型口罩的進貨量不超過![]() 型口罩的
型口罩的![]() 倍,設購進
倍,設購進![]() 型口罩
型口罩![]() 只,這
只,這![]() 只口罩的銷售總利潤為
只口罩的銷售總利潤為![]() 元.
元.
①求![]() 關于
關于![]() 的函數關系式;
的函數關系式;
②該藥店購進![]() 型、
型、![]() 型口罩各多少只,才能使銷售總利潤最大?
型口罩各多少只,才能使銷售總利潤最大?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線y=![]() x+c與x軸交于點B(4,0),與y軸交于點C,拋物線y=
x+c與x軸交于點B(4,0),與y軸交于點C,拋物線y=![]() x2+bx+c經過點B,C,與x軸的另一個交點為點A.
x2+bx+c經過點B,C,與x軸的另一個交點為點A.
(1)求拋物線的解析式;
(2)點P是直線BC下方的拋物線上一動點,求四邊形ACPB的面積最大時點P的坐標;
(3)若點M是拋物線上一點,請直接寫出使∠MBC=![]() ∠ABC的點M的坐標.
∠ABC的點M的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形![]() 的邊長為
的邊長為![]() ,延長
,延長![]() 至
至![]() 使
使![]() ,以
,以![]() 為邊長在上方作正方形
為邊長在上方作正方形![]() ,延長
,延長![]() 交
交![]() 于
于![]() ,連接
,連接![]() ,
,![]() ,
,![]() 為
為![]() 的中點,連接
的中點,連接![]() 分別與
分別與![]() 交于點
交于點![]()
![]() .則下列結論:①
.則下列結論:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正確的結論有( )
.其中正確的結論有( )
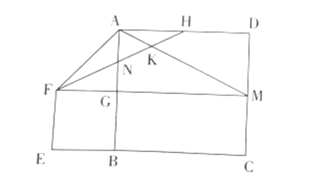
A.①②B.①④C.②③D.③④
查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com