
(8分)如圖,在△ABC中,∠ACB=90°,BC的垂直平分線DE交BC于D,交AB于E,F在DE上,并且AF=CE.

(1)求證:四邊形ACEF是平行四邊形;
(2)當∠B滿足什么條件時,四邊形ACEF是菱形?請回答并證明你的結論.
(1)證明見試題解析;(2)∠B=30°,證明見試題解析.
【解析】
試題分析:(1)易證∠DEC=∠DFA,即可得CE∥AF,根據CE=AF可得四邊形ACEF為平行四邊形;
(2)要使得平行四邊形ACEF為菱形,則AC=CE,又∵CE= AB,∴使得AB=2AC即可,根據AB、AC即可求得∠B的值.
AB,∴使得AB=2AC即可,根據AB、AC即可求得∠B的值.
試題解析:(1)∵DE為BC的垂直平分線,∴∠EDB=90°,BD=DC,
又∵∠ACB=90°,∴DE∥AC,∴E為AB的中點,∴在Rt△ABC中,CE=AE=BE,
∴∠AEF=∠AFE,且∠BED=∠AEF,∴∠DEC=∠DFA,∴AF∥CE,
又∵AF=CE,∴四邊形ACEF為平行四邊形;
(2)要使得平行四邊形ACEF為菱形,則AC=CE即可,
∵DE∥AC,∴∠BED=∠BAC,∠DEC=∠ECA,
又∵∠BED=∠DEC,∴∠EAC=∠ECA,∴AE=EC,又EB=EC,∴AE=EC=EB,
∵CE= AB,∴AC=
AB,∴AC= AB即可,
AB即可,
在Rt△ABC中,∠ACB=90°,∴當∠B=30°時,AB=2AC,
故∠B=30°時,四邊形ACEF為菱形.

考點:1.菱形的判定;2.線段垂直平分線的性質;3.平行四邊形的判定.


 考前必練系列答案
考前必練系列答案科目:初中數學 來源:2014-2015學年福建省、三中、城關小學九年級上學期期中聯考數學試卷(解析版) 題型:解答題
(12分)某水果批發商場經銷一種高檔水果,如果每千克盈利10元,每天可售出500千克.經市場調查發現,在進貨價不變的情況下,若每千克漲價1元,日銷售量將減少20千克.
(1)設每天盈利w元,求出w關于x的函數關系式,并說明每天盈利是否可以達到8000元?(6分)
(2)若該商場要保證每天盈利6000元,同時又要使顧客得到實惠,那么每千克應漲價多少元?(6分)
查看答案和解析>>
科目:初中數學 來源:2014-2015學年福建省漳州立人學校八年級上學期期中考試數學試卷(解析版) 題型:填空題
一個直角三角形的兩直角邊長分別為5cm和12cm,則斜邊長為 cm.
查看答案和解析>>
科目:初中數學 來源:2014-2015學年福建省九年級上學期期中質量監測數學試卷(解析版) 題型:選擇題
攝影興趣小組的學生,將自己拍攝的照片向本組其他成員各贈送一張,全組共互贈了182張,若全組有x名學生,則根據題意列出的方程是( )
A. B.
B.
C. D.
D.
查看答案和解析>>
科目:初中數學 來源:2014-2015學年福建省九年級上學期期中質量監測數學試卷(解析版) 題型:解答題
(6分)已知,AB和DE是直立在地面上的兩根立柱,AB=5m,某一時刻AB在陽光下的投影BC=3m.
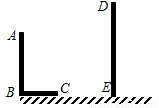
(1)請你在圖中畫出此時DE在陽光下的投影;
(2)在測量AB的投影時,同時測量出DE在陽光下的投影長為6m,請你計算DE的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com