
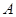 型桌椅售價150元,生產成本100元,運費2元;每套
型桌椅售價150元,生產成本100元,運費2元;每套 型桌椅售價200元,生產成本120元,運費4元,求總利潤
型桌椅售價200元,生產成本120元,運費4元,求總利潤 (元)與生產
(元)與生產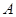 型桌椅
型桌椅 (套)之間的關系式,并確定總利潤最少的方案和最少的總利潤。(利潤
(套)之間的關系式,并確定總利潤最少的方案和最少的總利潤。(利潤 售價-生產成本-運費)
售價-生產成本-運費)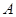 型桌椅246套、
型桌椅246套、 型桌椅254套時,總利潤
型桌椅254套時,總利潤 有最小值31118元;
有最小值31118元; ,最多為5名學生提供桌椅.
,最多為5名學生提供桌椅.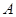 型桌椅
型桌椅 套,則生產
套,則生產 型桌椅
型桌椅 套,由題意得
套,由題意得

 ,
, 隨
隨 的增大而減少
的增大而減少 當
當 時,
時, 有最小值.
有最小值. 當生產
當生產 型桌椅246套、
型桌椅246套、 型桌椅254套時,總利潤
型桌椅254套時,總利潤 有最小值31118(元);
有最小值31118(元);

 精英口算卡系列答案
精英口算卡系列答案科目:初中數學 來源:不詳 題型:填空題
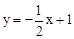 的圖象與x軸交于A、與y軸交于點B,點C在直線AB上,且OC=
的圖象與x軸交于A、與y軸交于點B,點C在直線AB上,且OC= AB,反比例函數
AB,反比例函數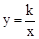 的圖象經過點C,則所有可能的k值為 .
的圖象經過點C,則所有可能的k值為 .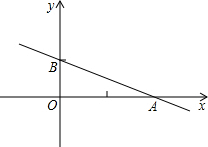
查看答案和解析>>
科目:初中數學 來源:不詳 題型:單選題
 的圖象在第一象限內的交點,點B在x軸負半軸上,且OA=OB,則△AOB的面積為( )
的圖象在第一象限內的交點,點B在x軸負半軸上,且OA=OB,則△AOB的面積為( )
| A.2 | B. | C.2 | D.4 |
查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題

 ?
?查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com