【題目】閱讀：在用尺規作線段
等于線段
時，小明的具體做法如下：
已知：如圖，線段.
求作：線段，使得線段
.
作法: ① 作射線
；
② 在射線上截取.
∴線段為所求.
解決下列問題：
已知：如圖，線段
.
（1）請你仿照小明的作法，在上圖中的射線上作線段
，使得
；（不要求寫作法和結論，保留作圖痕跡）
（2）在（1）的條件下，取
的中點
.若
，求線段
的長.（要求：第（2）問重新畫圖解答）
科目：初中數學 來源： 題型：
【題目】某中學九（1）班為了了解全班學生喜歡球類活動的情況，采取全面調查的方法，從足球、乒乓球、籃球、排球等四個方面調查了全班學生的興趣愛好，根據調查的結果組建了4個興趣小組，并繪制成如圖所示的兩幅不完整的統計圖（如圖①，②，要求每位學生只能選擇一種自己喜歡的球類），請你根據圖中提供的信息解答下列問題：
（1）九（1）班的學生人數為40，并把條形統計圖補充完整；
（2）扇形統計圖中m=10，n=20，表示“足球”的扇形的圓心角是72度；
（3）排球興趣小組4名學生中有3男1女，現在打算從中隨機選出2名學生參加學校的排球隊，請用列表或畫樹狀圖的方法求選出的2名學生恰好是1男1女的概率．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】我們把解相同的兩個方程稱為同解方程.例如：方程：
與方程
的解都為
，所以它們為同解方程.
(1)若方程
與關于
的方程
是同解方程，求
的值；
(2)若關于的方程
和
是同解方程，求的值；
(3)若關于的方程
和
是同解方程，求
的值.
查看答案和解析>>
科目：初中數學 來源： 題型：
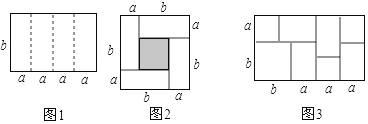
【題目】如圖1是一個長為4a、寬為b的長方形，沿圖中虛線用剪刀平均分成四塊小長方形，然后用四塊小長方形拼成一個“回形”正方形（如圖2）
（1）觀察圖2請你寫出（a+b）2、（a﹣b）2、ab之間的等量關系是_____；
（2）根據（1）中的結論，若x+y=5，xy=
，則x﹣y=______；
（3）若（3x﹣2y）2=5，（3x+2y）2=9，求xy的值．
（4）實際上通過計算圖形的面積可以探求相應的等式．如圖3，你有什么發現？_____．
查看答案和解析>>
科目：初中數學 來源： 題型：
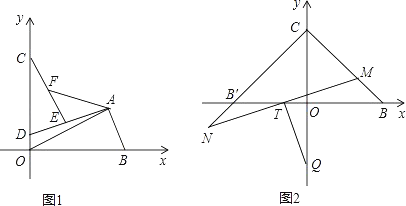
【題目】如圖，直角坐標系中，點B（a，0），點C（0，b），點A在第一象限．若a，b滿足（a﹣t）2+|b﹣t|=0（t＞0）．
（1）證明：OB=OC.
（2）如圖1，連接AB，過A作AD⊥AB交y軸于D，在射線AD上截取AE=AB，連接CE，F是CE的中點，連接AF，OA，當點A在第一象限內運動（AD不過點C）時，證明：∠OAF的大小不變.
（3）如圖2，B′與B關于y軸對稱，M在線段BC上，N在CB′的延長線上，且BM=NB′，連接MN交x軸于點T，過T作TQ⊥MN交y軸于點Q，求點Q的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某縣教育局為了豐富初中學生的大課間活動，要求各學校開展形式多樣的陽光體育活動．某中學就“學生體育活動興趣愛好”的問題，隨機調查了本校某班的學生，并根據調查結果繪制成如下的不完整的扇形統計圖和條形統計圖：
（1）在這次調查中，喜歡籃球項目的同學有 人，在扇形統計圖中，“乒乓球”的百分比為 %，如果學校有800名學生，估計全校學生中有 人喜歡籃球項目．
（2）請將條形統計圖補充完整．
（3）在被調查的學生中，喜歡籃球的有2名女同學，其余為男同學．現要從中隨機抽取2名同學代表班級參加校籃球隊，請直接寫出所抽取的2名同學恰好是1名女同學和1名男同學的概率．
查看答案和解析>>
科目：初中數學 來源： 題型：
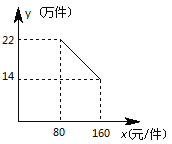
【題目】某公司去年年初投資1200萬元購買新生產線生產新產品，此外，生產每件該產品還需要成本60元，按規定，該產品售價不得低于80元/件且不超過160元/件，該產品的年銷售量y（萬件）與產品售價x（元/件）之間的關系如圖所示．
（1）求y與x的函數關系式，并寫出x的取值范圍；
（2）求該公司去年所獲利潤的最大值；
（3）在去年獲利最大的前提下，公司今年重新確定產品的售價，能否使去年和今年共獲利1000萬元？若能，請求出今年的產品售價；若不能，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】為了豐富同學的課余生活，某學校將舉行“親近大自然”戶外活動，現隨機抽取了部分學生進行主題為“你最想去的景點是________”的問卷調查，要求學生只能從“A（綠博園），B（人民公園），C（濕地公園），D（森林公園）”四個景點中選擇一項，根據調查結果，繪制了如下兩幅不完整的統計圖．
回答下列問題：
（1）本次共調查了多少名學生？
（2）補全條形統計圖；
（3）若該學校共有3 600名學生，試估計該校去濕地公園的學生人數．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】觀察下列計算過程，猜想立方根.
=1 
=8 
=27 
=64 
=125 
=216 
=343 
=512 
=729
（1）小明是這樣試求出19683的立方根的，先估計19683的立方根的個位數, 猜想它的個位數為 , 又由
<19000< 
，猜想19683的立方根十位數為 ，驗證得19683的立方根是 .
（2）請你根據（1）中小明的方法，完成如下填空：
① 
= ； ②
= ；③
= .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
