
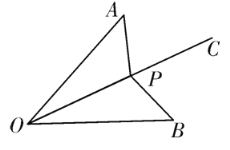
【題目】如圖,已知射線OC為∠AOB的平分線,且OA=OB,點P是射線OC上的任意一點,連接AP、BP.
(1)求證:△AOP≌△BOP;
(2)若∠AOB=50°,且點P是△AOB的外心,求∠APB的度數;
(3)若∠AOB=50°,且△OAP為鈍角三角形,直接寫出∠OAP的取值范圍.
【答案】(1)證明見解析;(2)∠APB=100°;(3)0°<∠OAP< 65°或90°<∠OAP<155°.
【解析】
(1)根據“SAS”證明即可;
(2)根據三角形外心定義得到PA=PB=PO,根據等腰三角形性質和三角形的外角性質求出∠APC=50°,根據∠APO=∠BPO即可求解;
(3)根據題意得![]() ,分
,分![]() 為鈍角和
為鈍角和![]() 為鈍角兩種情況討論即可.
為鈍角兩種情況討論即可.
解:(1)∵OP平分∠AOB,
∴∠AOP=∠BOP,
又∵OA=OB,OP=OP,
∴△AOP≌△BOP;
(2)∵∠AOB=50°,
∴∠AOP=∠BOP=25°,
∵點P是△AOB的外心,
∴PA=PB=PO,
∴∠A=∠AOP=25°,
∴∠APC=∠A+∠AOP=50°,
∵△AOP≌△BOP,
∴∠APO=∠BPO,
∴∠BPC=∠APC=50°,
∴∠APB=100°;
(3)∵∠AOB=50°,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
如圖1,當![]() 為鈍角時,
為鈍角時,
90°<∠OAP<155° ;
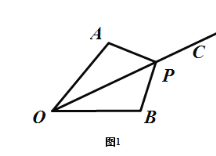
如圖2,當![]() 為鈍角時,
為鈍角時,
90°<∠OPA<155°,
即90°<![]() <155°,
<155°,
∴0°<∠OAP< 65°

∴∠OAP的取值范圍為:90°<∠OAP<155°或0°<∠OAP< 65°.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
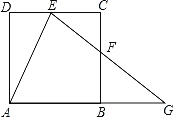
【題目】如圖,在正方形ABCD中,點E在DC邊上(不與點C,點D重合),點G在AB的延長線上,連結EG,交邊BC于點F,且EG=AG,連結AE,AF,設∠AED=![]() ,∠GFB=
,∠GFB=![]() .
.
(1)求![]() ,
,![]() 之間等量關系;
之間等量關系;
(2)若△ADE≌△ABF,AB=2,求BG的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
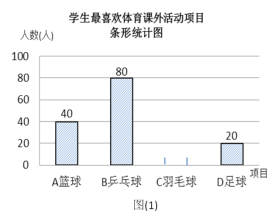
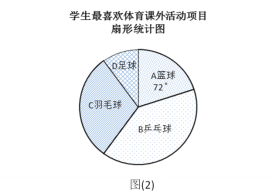
【題目】某學校為了豐富學生課余生活,決定開設以下體育課外活動項目:A籃球;B乒乓球;C羽毛球;D足球,為了解學生最喜歡哪一種活動項目,隨機抽取了部分學生進行調查,并將調查結果繪制成了兩幅不完整的統計圖,請回答下列問題:
(1)這次被調查的學生共有__________人;
(2)請你將條形統計圖(1)補充完整;
(3)在平時的乒乓球項目訓練中,甲、乙、丙、丁四人表現優秀,現決定從這四名同學中任選兩名參加乒乓球比賽,求恰好選中甲、乙兩位同學的概率(用樹狀圖或列表法解答)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學舉行鋼筆書法大賽,對各年級同學的獲獎情況進行了統計,并繪制了如下兩幅不完整的統計圖.
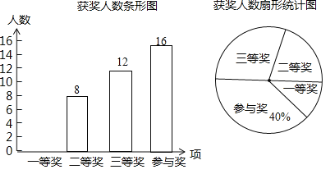
請結合圖中相關信息解答下列問題:
(1)扇形統計圖中三等獎所在扇形的圓心角的度數是______度;
(2)請將條形統計圖補全;
(3)獲得一等獎的同學中有![]() 來自七年級,有
來自七年級,有![]() 來自九年級,其他同學均來自八年級.現準備從獲得一等獎的同學中任選2人參加市級鋼筆書法大賽,請通過列表或畫樹狀圖的方法求所選出的2人中既有八年級同學又有九年級同學的概率.
來自九年級,其他同學均來自八年級.現準備從獲得一等獎的同學中任選2人參加市級鋼筆書法大賽,請通過列表或畫樹狀圖的方法求所選出的2人中既有八年級同學又有九年級同學的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點A,B為反比例函數y=![]() 在第一象限上的兩點,AC⊥y軸于點C,BD⊥x軸于點D,若B點的橫坐標是A點橫坐標的一半,且圖中陰影部分的面積為k﹣2,則k的值為( )
在第一象限上的兩點,AC⊥y軸于點C,BD⊥x軸于點D,若B點的橫坐標是A點橫坐標的一半,且圖中陰影部分的面積為k﹣2,則k的值為( )
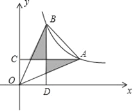
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
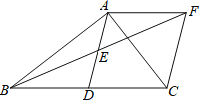
【題目】如圖,在![]() ABC中,AD是BC邊上的中線,點E是AD的中點,過點A作AF∥BC交BE的延長線于F,連接CF.
ABC中,AD是BC邊上的中線,點E是AD的中點,過點A作AF∥BC交BE的延長線于F,連接CF.
(1)求證:![]() AEF≌△DEB;
AEF≌△DEB;
(2)若∠BAC=90°,求證:四邊形ADCF是菱形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠ABC=90°,AB=4![]() ,∠CAB=30°,以AB的中點為圓心,OA的長為半徑作半圓交AC于點D,則圖中陰影部分的面積為_____.
,∠CAB=30°,以AB的中點為圓心,OA的長為半徑作半圓交AC于點D,則圖中陰影部分的面積為_____.
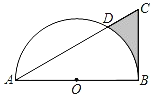
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】港口 A、B、C 依次在同一條直線上,甲、乙兩艘船同時分別從 A、B兩港出發,勻速駛向 C 港,甲、乙兩船與 B 港的距離 y(海里)與行駛時間 x 時)之間的函數關系如圖所示,則下列說法錯誤的是( )
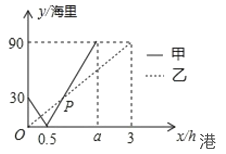
A.甲船平均速度為 60 海里/時B.乙船平均速度為 30 海里/時
C.甲、乙兩船在途中相遇兩次D.A、C 兩港之間的距離為 120 海里
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在![]() 中,
中,![]() ,
,![]() 是邊
是邊![]() 上的一點(不與點
上的一點(不與點![]() 重合),邊
重合),邊![]() 上點
上點![]() 在點
在點![]() 的右邊且
的右邊且![]() ,點
,點![]() 關于直線
關于直線![]() 的對稱點為
的對稱點為![]() ,連接
,連接![]() .
.
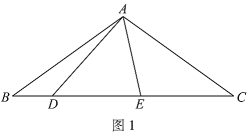
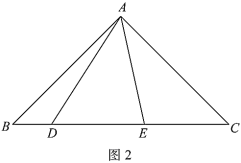
(1)如圖1,
①依題意補全圖1;
②求證:![]() ;
;
(2)如圖2,![]() ,用等式表示線段
,用等式表示線段![]() ,
,![]() ,
,![]() 之間的數量關系,并證明.
之間的數量關系,并證明.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com