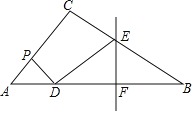
【題目】如圖，在△ABC中，∠C=
，點P在AC上運動，點D在AB上，PD始終保持與PA相等，BD的垂直平分線交BC于點E，交BD于點F，連接DE．若AC=6，BC=8，PA=2，則線段DE的長為________
【答案】
【解析】
連接OD，根據等腰三角形的性質得到∠A＝∠PDA，根據線段垂直平分線的性質得到EB＝ED，于是得到DE⊥DP；連接PE，設DE＝x，則EB＝ED＝x，CE＝8x，根據勾股定理即可得到結論．
∵PD＝PA，
∴∠A＝∠PDA，
∵EF是BD的垂直平分線，
∴EB＝ED，
∴∠B＝∠EDB，
∵∠C＝90°，
∴∠A＋∠B＝90°，
∴∠PDA＋∠EDB＝90°，
∴∠PDE＝180°90°＝90°，
∴DE⊥DP，
連接PE，
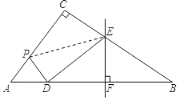
設DE＝x，則EB＝ED＝x，CE＝8x，
∵∠C＝∠PDE＝90°，
∴PC2＋CE2＝PE2＝PD2＋DE2，
∴42＋（8x）2＝22＋x2，
解得：x＝，
則DE＝．
科目：初中數學 來源： 題型：
【題目】如圖，在數軸上有A、B、C、D四個點，且線段AB=4，CD=6，已知A表示的數是﹣10，C表示的數是8，若線段AB以每秒6個單位長度的速度，線段CD以每秒2個單位長度的速度在數軸上運動（A在B左側，C在D左側）
（1）B，D兩點所表示的數分別是 、 ；
（2）若線段AB向右運動，同時線段CD向左運動，經過多少秒時，BC=2；
（3）若線段AB、CD同時向右運動，同時點P從原點出發以每秒1個單位長度的速度向右運動，經過多少秒時，點P到點A，C的距離相等？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】（1）先化簡，再求值： x﹣2（x﹣
y2）+（﹣2x+y2），其中x＝2，y＝﹣3
（2）已知：若a，b互為相反數，c，d互為倒數，m的絕對值為最小正整數，求代數式﹣2cd+
﹣m的值
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】觀察一組數據：2，4，7，11，16，22，29，…，它們有一定的規律，若記第一個數為a1，第二個數記為a2，…，第n個數記為an.
(1)請寫出29后面的第一個數；
(2)通過計算a2－a1，a3－a2，a4－a3，…由此推算a100－a99的值；
(3)根據你發現的規律求a100的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】將連續的奇數1、3、5、7、9，……排成如下的數表：
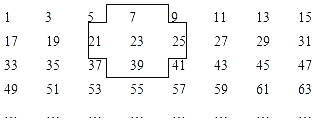
（1）十字框中的5個數的和與中間的數23有什么關系？若將十字框上下左右平移，可框住另外5個數，這5個數還有這種規律嗎？
（2）設十字框中中間的數為a，用含a的式子表示十字框中的其他四個數；
（3）十字框中的5個數的和能等于2018嗎？若能，請寫出這5個數；若不能，說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，△ABC中，∠C＝90°，D是BC邊上一點，∠ADC＝3∠BAD，BD＝8，DC＝7，則AB的值為（ ）
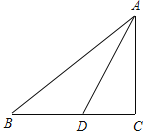
A. 15 B. 20 C. 2
+7 D. 2+
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖是張亮、李娜兩位同學零花錢全學期各項支出的統計圖．根據統計圖，下列對兩位同學購買書籍支出占全學期總支出的百分比作出的判斷中，正確的是（ ）
A. 張亮的百分比比李娜的百分比大 B. 張娜的百分比比張亮的百分比大
C. 張亮的百分比與李娜的百分比一樣大 D. 無法確定
查看答案和解析>>
科目：初中數學 來源： 題型：
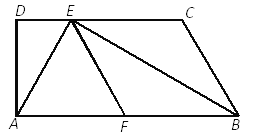
【題目】如圖，已知梯形ABCD中，AB∥CD，∠D=90°，BE平分∠ABC，交CD于點E，F是AB的中點，聯結AE、EF，且AE⊥BE．
求證：（1）四邊形BCEF是菱形；
（2）
.
查看答案和解析>>
科目：初中數學 來源： 題型：
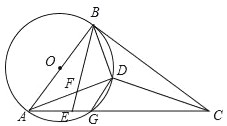
【題目】如圖：AB是⊙O的直徑，AC交⊙O于G，E是AG上一點，D為△BCE內心，BE交AD于F，且∠DBE=∠BAD．
（1）求證：BC是⊙O的切線；
（2）求證：DF=DG；
（3）若∠ADG=45°，DF=1，則有兩個結論：①ADBD的值不變；②AD－BD的值不變，其中有且只有一個結論正確，請選擇正確的結論，證明并求其值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com