
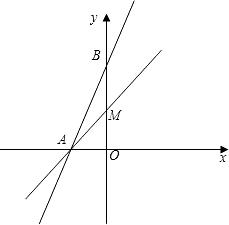
 如圖直線
如圖直線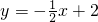 分別交x軸、y軸于點A和B,點P(t,0)是x軸上一動點,P、Q兩點關(guān)于直線AB軸對稱,PQ交AB于點M,作QH⊥x軸于點H.
分別交x軸、y軸于點A和B,點P(t,0)是x軸上一動點,P、Q兩點關(guān)于直線AB軸對稱,PQ交AB于點M,作QH⊥x軸于點H. x+2=0,解得x=4,
x+2=0,解得x=4, =
= =
= ;
; =
= =2
=2 ,
, =
= ,
, =
= ,
, =
= ,
, PQ=
PQ= ,
, ÷
÷ =
= ,
, =
= ,
, ,0),
,0), =
= ,
, ,0);
,0); ,0)或(
,0)或( ,0);
,0); (4-t),
(4-t), (4-t),
(4-t), (4-t)×
(4-t)× =
=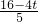 ,
, (4-t)×
(4-t)× =
= ,
, =
=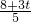 ,
,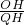 =
=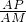 =tan∠OAB或
=tan∠OAB或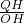 =
=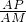 =tan∠OAB,
=tan∠OAB,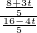 =
= 或
或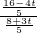 =
= ,
,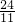 ;
; =-
=-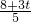 ,
,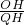 =
=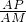 =tan∠OAB或
=tan∠OAB或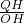 =
=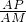 =tan∠OAB,
=tan∠OAB,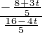 =
= 或
或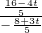 =
= ,
, (t-4),
(t-4), (t-4),
(t-4), (t-4)×
(t-4)× =
=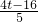 ,
, (t-4)×
(t-4)× =
= ,
, =
=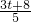 ,
,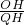 =
=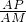 =tan∠OAB或
=tan∠OAB或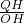 =
=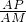 =tan∠OAB,
=tan∠OAB,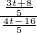 =
= 或
或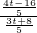 =
= ,
,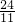 或t=-16或t=8,使△OQH與△APM相似.
或t=-16或t=8,使△OQH與△APM相似.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應(yīng)用題系列答案
小學生10分鐘應(yīng)用題系列答案科目:初中數(shù)學 來源: 題型:
 y軸正半軸與點M,且點M為線段OB的中點.
y軸正半軸與點M,且點M為線段OB的中點.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
 如圖,在平面直角坐標系中,函數(shù)y=2x+12的圖象分別交x軸、y軸于A、B兩點.過點A的直線交y軸正半軸于點C,且點C為線段OB的中點.
如圖,在平面直角坐標系中,函數(shù)y=2x+12的圖象分別交x軸、y軸于A、B兩點.過點A的直線交y軸正半軸于點C,且點C為線段OB的中點.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
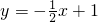 分別與x軸、y軸交于點A、B,在第一象限取點C,使△ABC成為等腰直角三角形;如果在第二象限內(nèi)有一點P(a,
分別與x軸、y軸交于點A、B,在第一象限取點C,使△ABC成為等腰直角三角形;如果在第二象限內(nèi)有一點P(a, ),使△ABP的面積與Rt△ABC的面積相等,求a的值.
),使△ABP的面積與Rt△ABC的面積相等,求a的值.
查看答案和解析>>
科目:初中數(shù)學 來源:2012年浙江省金華五中中考數(shù)學模擬試卷(5月份)(解析版) 題型:解答題
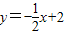 分別交x軸、y軸于點A和B,點P(t,0)是x軸上一動點,P、Q兩點關(guān)于直線AB軸對稱,PQ交AB于點M,作QH⊥x軸于點H.
分別交x軸、y軸于點A和B,點P(t,0)是x軸上一動點,P、Q兩點關(guān)于直線AB軸對稱,PQ交AB于點M,作QH⊥x軸于點H.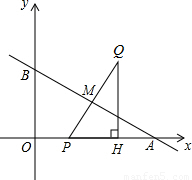
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com